Câu hỏi/bài tập:

Cho tam giác ABC cân tại đỉnh A. Hai đường phân giác BE và CF của tam giác ABC cắt nhau tại điểm I. Chứng minh rằng
a) ΔBIC $\backsim $ ΔEIF
b) $F{{B}^{2}}=FI.FC$
c) Cho biết AB = 6cm, BC = 3 cm. Tính EF

a) Sử dụng định lý Thales đảo chứng minh EF // BC
b) Sử dụng các tỉ số đồng dạng của hai tam giác để chứng minh $F{{B}^{2}}=FI.FC$
c) Dựa vào định lý Thales cho EF // BC, ta có các tỉ số bằng nhau suy ra độ dài EF.
Advertisements (Quảng cáo)

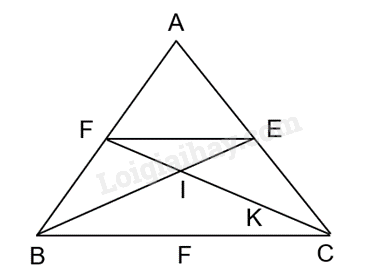
a) Do BE là đường phân giác của góc B nên $\widehat{{{B}_{1}}}=\widehat{{{B}_{2}}}$, ta có: $\frac{EA}{EC}=\frac{BA}{BC}$ (1).
Tương tự với đường phân giác CF, ta có: $\frac{FA}{FB}=\frac{CA}{CB}$ (2).
Bởi vậy, từ (1) và (2) ta suy ra $\frac{EA}{EC}=\frac{FA}{FB}$, nghĩa là EF định ra trên hai cạnh AB và AC những đoạn thẳng tương ứng tỉ lệ. Do đó theo định lý Thales đảo ta có EF // BC. Từ đó suy ra $\Delta BIC\backsim \Delta EIF$ (đpcm).
b) Hai tam giác BFI và CFB có $\widehat{F}$ chung, $\widehat{{{B}_{1}}}=\frac{\widehat{ABC}}{2}=\frac{\widehat{ACB}}{2}=\widehat{{{C}_{2}}}$.
Do đó $\Delta BFI\backsim \Delta CFB\Rightarrow \frac{FB}{FC}=\frac{FI}{FB}\Rightarrow F{{B}^{2}}=FI.FC$ (đpcm).
c) Ta có EF // BC (chứng minh trên). Do đó: $\frac{BC}{EF}=\frac{AB}{AF}\Rightarrow \frac{BC}{EF}=\frac{\left( AF+FB \right)}{AF}=1+\frac{BC}{AB}=1+\frac{3}{6}=\frac{3}{2}$.
Từ đó suy ra EF = 3: $\frac{3}{2}$ = 2 (cm).
