Câu hỏi/bài tập:

Cho các đơn thức:
\(A = 4x\left( { - 2} \right){x^2}y;B = 12,75xyz;C = (1 + 2.4,5){x^2}y\frac{1}{5}{y^3};D = \left( {2 - \sqrt 5 } \right)x.\)
a) Liệt kê các đơn thức thu gọn trong các đơn thức đã cho và thu gọn các đơn thức còn lại.
b) Với mỗi đơn thức nhận được, hãy cho biết hệ số, phần biến và bậc của nó.

a) Sử dụng khái niệm đơn thức thu gọn: Đơn thức thu gọn là đơn thức chỉ gồm một số, hoặc có dạng tích của một số với những biến, mỗi biến chỉ xuất hiện một lần và đã được nâng lên lũy thừa với số mũ nguyên dương.
Advertisements (Quảng cáo)
b) Trong một đơn thức thu gọn, phần số còn gọi là hệ số, phần còn lại gọi là phần biến.
Tổng số mũ của các biến trong một đơn thức thu gọn với hệ số khác 0 gọi là bậc của đơn thức đó.

a) Các đơn thức thu gọn là \(B = 12,75xyz\) ; \(D = \left( {2 - \sqrt 5 } \right)x\) . Ta thu gọn hai đơn thức còn lại:
\(\begin{array}{l}A = 4x\left( { - 2} \right){x^2}y = \left[ {4.\left( { - 2} \right)} \right].(x.{x^2}).y = - 8{x^3}y;\\C = (1 + 2.4,5){x^2}y\frac{1}{5}{y^3} = 10{x^2}y.\frac{1}{5}{y^3}\\ = \left( {10.\frac{1}{5}} \right).{x^2}.\left( {y.{y^3}} \right) = 2{x^2}{y^4}\end{array}\)
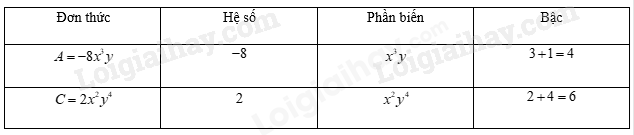
b) Hệ số, phần biến và bậc của từng đơn thức được ghi lại trong bảng sau: