Sử dụng tính chất của đường trung bình. Sử dụng dấu hiệu nhận biết hình bình hành, hình thoi. Giải chi tiết Giải bài 3 trang 61 vở thực hành Toán 8 - Bài 14. Hình thoi và hình vuông . Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của hình thoi
Câu hỏi/bài tập:

Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của hình thoi

- Sử dụng tính chất của đường trung bình.
- Sử dụng dấu hiệu nhận biết hình bình hành, hình thoi.
Advertisements (Quảng cáo)

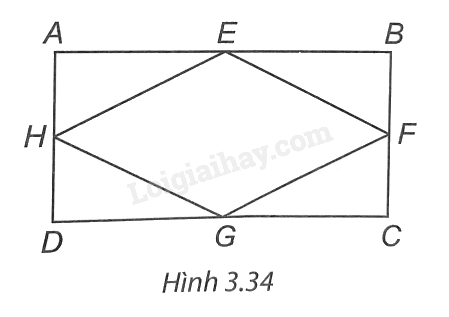
(H.3.34). Ta có \(AE{\rm{ }} = \;EB,\;AH{\rm{ }} = \;HD\; \Rightarrow \;HE{\rm{ }}//\;BD,\;HE{\rm{ }} = \;\frac{1}{2}BD\).
Tương tự \(GF{\rm{ }}//\;BD,{\rm{ }}GF{\rm{ }} = \;\;\frac{1}{2}BD,\;EF{\rm{ }}//\;AC,\;EF{\rm{ }} = \;\frac{1}{2}AC\).
Suy ra HE // GF, HE = GF, do đó HEFG là hình bình hành.
Tứ giác ABCD là hình chữ nhật nên AC = BD ⇒ HE = GF = EF = HG ⇒ HEFG là hình thoi.
