Bài 4 trang 55 vở thực hành Toán 8: Cho hình bình hành ABCD. Lấy điểm E sao cho B là trung điểm của AE...

Cho hình bình hành ABCD. Lấy điểm E sao cho B là trung điểm của AE, lấy điểm F sao cho C là trung điểm của DF. Chứng minh rằng:

a) Hai tứ giác AEFD, ABFC là những hình bình hành.

b) Các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.

a) Dựa vào dấu hiệu nhận biết hình bình hành để chứng minh.

b) Dựa vào tính chất của hình bình hành: Các đường chéo cắt nhau tại trung điểm suy ra các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.

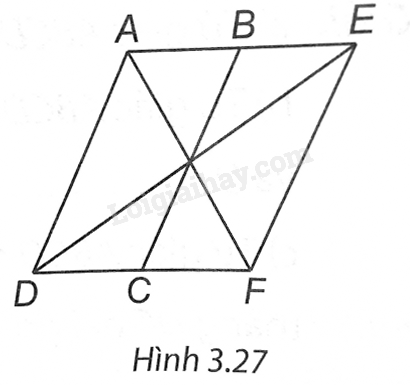
(H.3.27). a) Do ABCD là hình bình hành nên AB // CD, DC = AB, suy ra AE // DF, AE = 2AB = 2CD = DF.

⇒ AEFD là hình bình hành.

Tương tự, tứ giác ABFC có các cạnh đối song song và bằng nhau nên ABFC là hình bình hành.

b) Vì AEFD là hình bình hành nên AF cắt ED tại trung điểm mỗi đường.

Vì ABFC là hình bình hành nên AF cắt BC tại trung điểm mỗi đường.

Vậy ba trung điểm của AF, DE, BC trùng nhau.