Bài 5 trang 49 vở thực hành Toán 8: Cho hình thang cân ABCD có đáy nhỏ BHạ BH ⊥ AD, CE ⊥ AD. Chứng minh AH = ED...

Cho hình thang cân ABCD có đáy nhỏ BC. Hạ BH ⊥ AD, CE ⊥ AD.

a) Chứng minh AH = ED.

b) Cho BH = 4 cm, và $\widehat A = 45^\circ .$ Tính độ dài ED.

a) Dựa vào tính chất của hình thang cân và chứng minh $\Delta ABH = \Delta DCE$ suy ra AH = ED (hai cạnh tương ứng).

b) Chứng minh tam giác ABH vuông cân tại H suy ra độ dài các cạnh tương ứng, ta tính được độ dài ED.

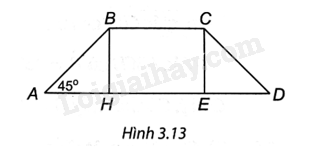
a) Ta có hình thang ABCD cân nên $\widehat D = \widehat A,AB = CD$.

Xét hai tam giác vuông ABH và DCE có: $\widehat D = \widehat A,AB = CD$, do đó $\Delta ABH = \Delta DCE$ (cạnh huyền – góc nhọn). Từ đó suy ra AH = ED.

b) Ta có $\widehat A = {45^0},BH \bot AD$ nên tam giác ABH vuông cân tại H.

$\Rightarrow AH = BH$ mà $AH = ED \Rightarrow ED = BH = 4cm$ (chứng minh trên).

Vậy ED = 4 cm.