Câu hỏi/bài tập:

Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho AM = AN.
a) Tính số đo góc AMN theo góc A.
b) Tứ giác BMNC là hình gì? Vì sao?
c) Cho BM = MN = NC, chứng minh BN là phân giác của góc ABC, CM là phân giác của góc ACB.

a) Dựa vào tính chất tam giác cân?
b) Sử dụng dấu hiệu nhận biết hình thang cân.
c) Sử dụng tính chất của tam giác cân để chứng minh.
Advertisements (Quảng cáo)

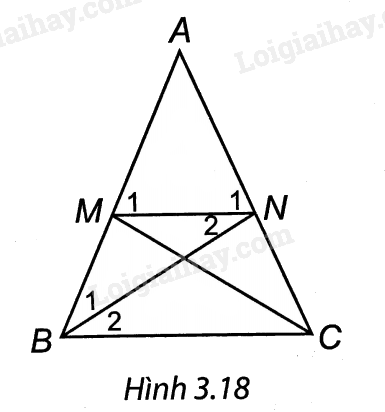
(H.3.18). a) Ta có AM = AN (giả thiết) nên ∆AMN cân tại A
\( \Rightarrow {\widehat M_1} = {\widehat N_1} = \frac{{180^\circ - \widehat A}}{2}.\)
b) Vì ∆ABC cân tại A nên \(\widehat B = \widehat C = \frac{{180^\circ - \widehat A}}{2}.\)
Suy ra \({\widehat M_1} = \widehat B \Rightarrow \) MN // BC (do có cặp góc đồng vị bằng nhau), từ đó tứ giác BMNC là hình thang.
Mặt khác \(\widehat B = \widehat C\) nên BMNC là hình thang cân.
c) Ta có BM = MN ⇒ ∆BMN cân tại M \( \Rightarrow {\widehat B_1} = {\widehat N_2}.\)
Do MN // BC nên \({\widehat B_2} = {\widehat N_2}\) (hai góc so le trong). Từ đó suy ra \({\widehat B_1} = {\widehat B_2},\) tức BN là tia phân giác của góc ABC.
Tương tự ta chứng minh được CM là tia phân giác của góc ACB.
