Câu hỏi/bài tập:

Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Một đường thẳng đi qua O lần lượt cắt các cạnh AB, CD của hình bình hành tại hai điểm M, N. Chứng minh ∆OAM = ∆OCN. Từ đó suy ra tứ giác MBND là hình bình hành.

Chứng minh ∆OAM = ∆OCN theo trường hợp góc – cạnh – góc.
Dựa vào dấu hiệu nhận biết tứ giác có hai đường chéo cắt nhau tại trung điểm là hình bình hành, ta chứng minh được MBND là hình bình hành.
Advertisements (Quảng cáo)

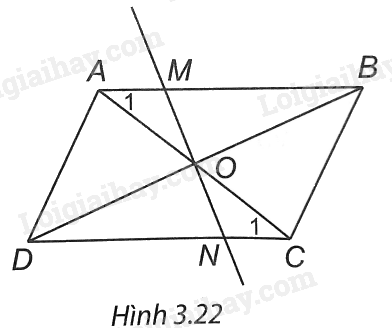
(H.3.22). ABCD là hình bình hành nên AO = CO, BO = DO.
Xét ∆OAM và ∆OCN có: \(\widehat {OAM} = \widehat {OCN}\) (hai góc so le trong), \(\widehat {AOM} = \widehat {CON}\) (hai góc đối đỉnh), AO = CO nên ∆OAM = ∆OCN (g.c.g).
Suy ra OM = ON.
Ta có OM = ON, BO = DO nên tứ giác MBND có hai đường chéo MN, BD cắt nhau tại trung điểm mỗi đường nên MBND là hình bình hành.
