Câu hỏi/bài tập:

Cho tam giác nhọn ABC có trực tâm H. Vẽ các đường thẳng d vuông góc với AB tại B, d’ vuông góc với AC tại C, d và d’ cắt nhau tại N. Chứng mình rằng:
a) Tứ giác BHCN là hình bình hành.
b) HN đi qua trung điểm I của đoạn thẳng BC.

a) Dựa vào dấu hiệu nhận biết: Tứ giác có các cặp cạnh đối song song là hình bình hành để chứng minh BHCN là hình bình hành.
b) Vì BHCN là hình bình hành nên ta suy ra HN đi qua trung điểm I của đoạn thẳng BC.
Advertisements (Quảng cáo)

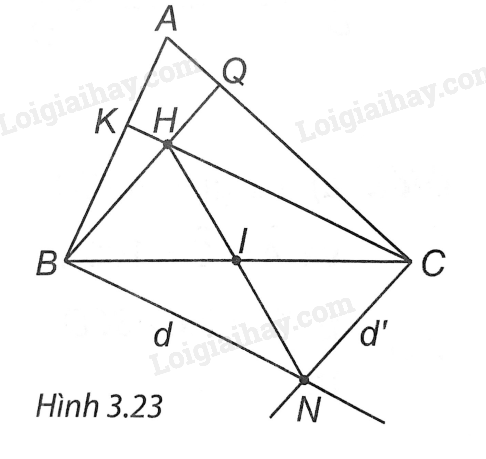
(H.3.23). Vì H là trực tâm của ∆ABC nên CH ⊥ AB, BH ⊥ AC.
Ta có CH ⊥ AB, NB ⊥ AB ⇒ CH // NB.
Tương tự BH // CN.
Từ đó, suy ra BHCN là hình bình hành.
b) Ta có BHCN là hình bình hành nên BC và HN cắt nhau tại trung điểm mỗi đường, do đó HN đi qua trung điểm I của đoạn thẳng BC.
