Câu hỏi/bài tập:

Cho tam giác ABC vuông tại A. Trên cạnh AB lấy điểm K, trên cạnh AC lấy điểm H sao cho BK = CH. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh KH, BH, BC, CK. Chứng minh rằng MNPQ là hình vuông.

MNPQ là hình bình hành ⇒ hình thoi ⇒ hình vuông.

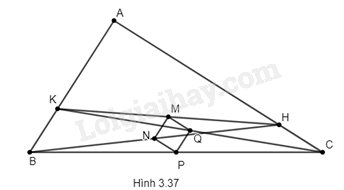
(H.3.37). Vì MK = MH, NB = NH ⇒ MN là đường trung bình trong tam giác HKB.
⇒ MN // KB và MN = \(\frac{1}{2}\)KB (1)
Advertisements (Quảng cáo)
Chứng minh tương tự, ta có:
PQ // KB và PQ = \(\frac{1}{2}\)KB (2)
NP // CH và NP = \(\frac{1}{2}\)CH (3)
Từ (1) và (2), ta có MN // PQ và MN = PQ ⇒ MNPQ là hình bình hành (4)
Ta có BK = CH (giả thiết). (5)
Từ (1), (3) và (5), ta có MN = NP ⇒ MNPQ là hình thoi (6)
Vì ∆ABC vuông tại A (giả thiết) ⇒ BK ⊥ CH, mà NP // CH, MN // KB (chứng minh trên).
⇒ MN ⊥ NP (7).
Từ (6) và (7), ta có MNPQ là hình thoi có một góc vuông nên nó là hình vuông.
