Câu hỏi/bài tập:

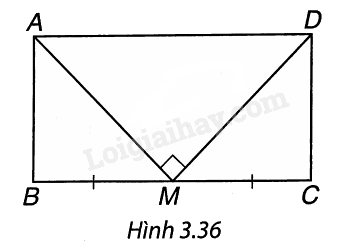
Cho hình chữ nhật ABCD có chu vi bằng 36 cm. Gọi M là trung điểm của cạnh BC. Biết rằng MA ⊥ MD. Tính độ dài các cạnh của hình chữ nhật ABCD (H.3.36).

- Chứng minh \(\Delta AMB = \Delta DMC\).
- Chứng minh AB = BM = MC = CD, ta tính được các cạnh của hình chữ nhật.

Advertisements (Quảng cáo)
Hai tam giác vuông AMB và DMC có AB = DC, BM = MC nên \(\Delta AMB = \Delta DMC(c.g.c) \Rightarrow \widehat {AMB} = \widehat {DMC}.\)
Do góc \(\widehat {AMD} = 90^\circ \Rightarrow \widehat {AMB} = \widehat {DMC} = \left( {180^\circ - 90^\circ } \right):2 = 45^\circ .\)
Do đó ∆AMB vuông cân tại B, ∆DMC vuông cân tại C.
Suy ra AB = BM = MC = CD.
Ta có AD = BC = 2AB, suy ra chu vi của ABCD bằng
AB + BC + CD + DA = 36
Do đó AB = CD = 36 : 6 = 6 cm, AD = CB = 12 cm.
