Câu hỏi/bài tập:

Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC còn P, N lần lượt là chân đường vuông góc hạ từ M xuống CA, AB (H.3.45). 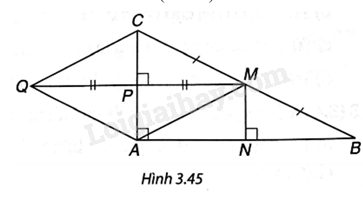
a) Chứng minh hai tam giác vuông CMP và MBN bằng nhau.
b) Chứng minh tứ giác APMN là một hình chữ nhật.
Từ đó suy ra N là trung điểm của AB, P là trung điểm của AC.
c) Lấy điểm Q sao cho P là trung điểm của MQ, chứng minh tứ giác AMCQ là một hình thoi.
d) Nếu AB = AC, tức là tam giác ABC vuông cân tại A thì tứ giác AMCQ có là hình vuông không? Vì sao?

a) Chứng minh ∆CMP = ∆MBN theo trường hợp cạnh huyền – góc nhọn.
b) Chứng minh tứ giác ANMP có ba góc vuông nên là hình chữ nhật.
c) Dựa vào dấu hiệu nhận biết để chứng minh AMCQ là hình thoi.
d) Chứng minh hình thoi AMCQ có một góc vuông là hình vuông.

Advertisements (Quảng cáo)
a) Ta có: PM ⊥ AC, AB ⊥ AC ⇒ PM // AB ⇒ \(\widehat {CMP} = \widehat {CBA}\) (hai góc đồng vị).
Hai tam giác vuông CMP và MBN có: CM = MB, \(\widehat {CMP} = \widehat {MBN}\) (chứng minh trên)
⇒ ∆CMP = ∆MBN (cạnh huyền – góc nhọn).
b) Tứ giác ANMP có ba góc vuông nên là hình chữ nhật.
⇒ PM = AN.
∆CMP = ∆MBN ⇒ PM = BN.
Từ đó, suy ra PM = AN = BN nên N là trung điểm của AB.
Tương tự, ta có CP = MN = AP, tức P là trung điểm của AC.
c) Tứ giác AMCQ có hai đường chéo AC và MQ cắt nhau tại trung điểm mỗi đường nên là hình bình hành, mà QM ⊥ AC nên AMCQ là một hình thoi.
d) Khi AB = AC, tức là tam giác ABC vuông cân tại A thì \(\widehat {ACB} = 45^\circ \).
⇒ \(\widehat {QCM} = 2\widehat {ACB} = 90^\circ \) (do AC là một đường chéo của hình thoi AMCQ).
Vậy hình thoi AMCQ có một góc vuông nên là hình vuông.
Vậy khi AB = AC thì tứ giác AMCQ là hình vuông.
