Câu hỏi/bài tập:
Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD (H.3.8).
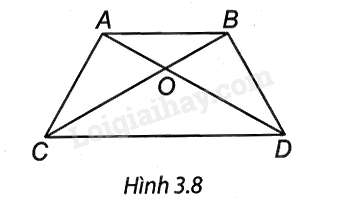
Trong các khẳng định sau, khẳng định sai là
A. BC = AD.
B. ABCD là hình thang cân.
C. AC = BD.
D. Tam giác AOC cân tại O.

- Dựa vào tính chất của hình thang cân:
Advertisements (Quảng cáo)
+ Định lý 1. Trong hình thang cân, hai cạnh bên bằng nhau.
+ Định lý 2. Trong hình thang cân, hai đường chéo bằng nhau.
- Dựa vào dấu hiệu nhận biết hình thang cân:
+ Định lý 3. Nếu một hình thang có hai đường chéo bằng nhau thì hình thang đó là hình thang cân.

Ta có: OA = OB; OC = OD suy ra OA + OC = OB + OD
Khi đó AC = BD nên ABCD là hình thang cân. Do đó B, C đúng.
ABCD là hình thang cân nên hai cạnh bên bằng nhau nên BD = AC. Do đó A đúng.
Vì A, O, C thẳng hàng nên D là khẳng định sai.
=> Chọn đáp án D.
