Kẻ đường cao CH và AK. Tính diện tích tam giác ABC và ACD. Do đó\({S_{ABCD}} = {S_{ABC}} + {S_{ACD}} = \frac{{AB. CH + DC. Giải và trình bày phương pháp giải Giải bài 10 trang 37 sách bài tập toán 9 - Cánh diều tập 1 - Bài 1. Bất đẳng thức . Cho tứ giác ABCD. Chứng minh diện tích của tứ giác ABCD không lớn hơn (frac{{AB.BC + AD.DC}}{2}.
Câu hỏi/bài tập:
Cho tứ giác ABCD. Chứng minh diện tích của tứ giác ABCD không lớn hơn \(\frac{{AB.BC + AD.DC}}{2}.\)
Kẻ đường cao CH và AK.
Tính diện tích tam giác ABC và ACD.
Do đó\({S_{ABCD}} = {S_{ABC}} + {S_{ACD}} = \frac{{AB.CH + DC.AK}}{2}\)
Kết hợp với điều kiện \(CH \le BC,AK \le AD\), ta được điều phải chứng minh.
Advertisements (Quảng cáo)
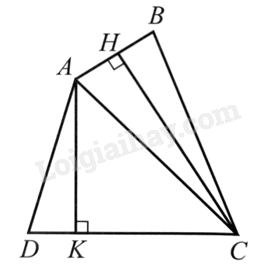
Kẻ \(CH \bot AB,AK \bot DC(H \in AB,K \in DC)\).
Ta có \({S_{ABC}} = \frac{{AB.CH}}{2},{S_{ACD}} = \frac{{DC.AK}}{2}\)
Do đó
\({S_{ABCD}} = {S_{ABC}} + {S_{ACD}} \\= \frac{{AB.CH}}{2} + \frac{{DC.AK}}{2} = \frac{{AB.CH + DC.AK}}{2}\)
Mà \(CH \le BC,AK \le AD\) suy ra \({S_{ABCD}} \le \frac{{AB.BC + AD.DC}}{2}\)
Vậy diện tích của tứ giác ABCD không lớn hơn \(\frac{{AB.BC + AD.DC}}{2}.\)