Câu hỏi/bài tập:

Một người lính cứu hoả dựng một chiếc thang dài 25 ft dựa vào tưởng với góc tạo bởi thang và phương nằm ngang là góc α. Biết đỉnh của chiếc thang cách mặt đất là 20 ft (Hình 30). Tính khoảng cách x từ chân thang đến chân tường và số đo góc α (làm tròn kết quả đến hàng đơn vị của độ).
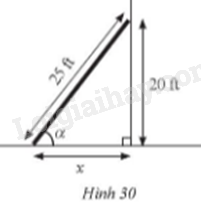

Áp dụng tỉ số lượng giác trong tam giác vuông để tính α và định lý Pythagore để tính x.

Advertisements (Quảng cáo)
Bài toán được mô tả như hình vẽ:
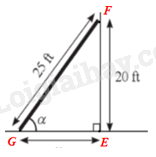
Độ dài thang \(GE = 25\)ft, góc tạo bỏi thang và phương nằm ngang là \(\widehat G = \alpha \), đỉnh thang cách mặt đất là \(EF = 25\)ft, khoảng cách từ chân tường đến chân thang là \(GE = x\).
Xét tam giác EGF vuông tại E, ta có:
\(\sin G = \frac{{EF}}{{GF}} = \frac{{20}}{{25}} = \frac{4}{5}\) nên \(\widehat G = \alpha \approx 53^\circ \).
và \(x = GE = \sqrt {G{E^2} - E{F^2}} \)(định lý Pythagore) hay \(x = GE = \sqrt {{{25}^2} - {{20}^2}} = 15\)ft.
