Câu hỏi/bài tập:

Một thuỷ thủ lái thuyền từ bờ (ở vị trí A) ra biển theo hướng Đông Bắc với góc nghiêng so với hướng Bắc là 41°. Đi được 2,8 km thì người đó phát hiện sắp hết nhiên liệu (ở vị trí B), vội quay thuyền vào bờ theo hướng Nam. Người đó đi tiếp được 1,8 km thì thuyền bị tắt máy (ở vị trí C) (Hình 31). Hỏi lúc đó thuyền còn cách bờ bao xa (làm tròn kết quả đến hàng phần mười của kilômét)?
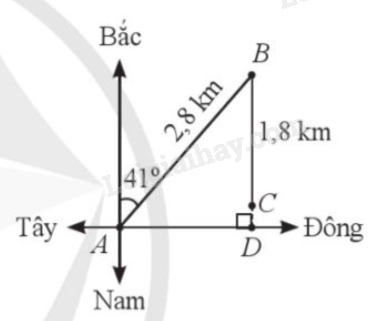

Bước 1: Áp dụng tỉ số lượng giác trong tam giác vuông ABD để tính BD.
Bước 2: Khoảng cách cần tìm: \(CD = BD - BC\).

Advertisements (Quảng cáo)
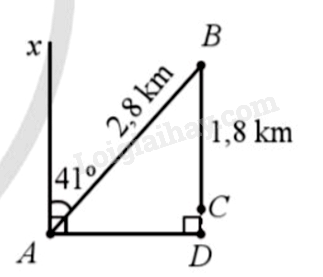
Gọi tia Ax là hướng Đông bắc.
Ta có: \(BD \bot DA,Ax \bot DA\) nên \(Ax//BD\).
Suy ra \(\widehat {xAB} = \widehat {ABD} = 41^\circ \).
Xét tam giác ABD vuông tại D có:
\(\cos B = \frac{{BD}}{{AB}}\) nên \(BD = AB.\sin B = 2,8.\cos 41^\circ \).
Khoảng cách giữa thuyền và bờ là:
\(CD = BD - BC = 2,8.\cos 41^\circ - 1,8 \approx 0,3\)km.
