Câu hỏi/bài tập:

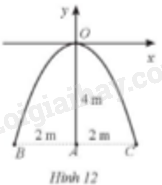
Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng \(y = a{x^2}\), gốc toạ độ O là vị trí cao nhất của cổng so với mặt đất, x và y được tính theo đơn vị mét. Chiều cao OA, chiều rộng BC của cổng đều là 4 m (Hình 12). Giả sử một chiếc xe tải có chiều cao 3 m đi vào chính giữa cổng (qua điểm A). Chiều ngang p của chiếc xe tải phải thoả mãn điều kiện gì để có thể đi qua cổng mà không chạm vào cổng?

Bước 1: Tìm a (dựa vào điểm \(C\left( {2; - 4} \right)\) thuộc đồ thị hàm số).
Bước 2: Ta thấy chiều ngang p là \(p = \left| {2x} \right|\) và khoảng cách từ nóc xe đến điểm cao nhất của cổng là 1m nên \(\left| { - {{\left( {\frac{p}{2}} \right)}^2}} \right| < 1\). Từ đó tìm được p.
Advertisements (Quảng cáo)

Dựa vào đồ thị ta thấy: Điểm \(C\left( {2; - 4} \right)\) thuộc đồ thị hàm số \(y = a{x^2}\) nên ta có \( - 4 = a{.2^2}\)
Hay \(a = - 1\). Suy ra hàm số có dạng \(y = - {x^2}\).
Gọi \(K\left( {0; - 1} \right)\) là điểm thuộc Oy. Để xe tải có chiều cao 3 m có chiều ngang p (tức là \(p = \left| {2x} \right|\)) đi vào chính giữa cổng mà không chạm vào cổng thì \(\left| { - {{\left( {\frac{p}{2}} \right)}^2}} \right| < 1\) hay \({p^2} < 4\).
Từ đó suy ra \( - 2 < p < 2\).
Vậy \( - 2 < p < 2\) là giá trị cần tìm.
