Lập bảng giá trị của hàm số. Vẽ đồ thị hàm số. Nhìn đồ thị để kết luận. Vận dụng kiến thức giải Giải bài 3 trang 7 sách bài tập toán 9 - Chân trời sáng tạo tập 2 - Bài 1. Hàm số và đồ thị của hàm số y = ax² (a ≠ 0) . Cho parabol (P): y = (frac{3}{2})x2 và đường thẳng d: y = 3x.
Câu hỏi/bài tập:

Cho parabol (P): y = \(\frac{3}{2}\)x2 và đường thẳng d: y = 3x.
a) Vẽ (P) và d trên cùng một mặt phẳng toạ độ Oxy.
b) Dựa vào hình vẽ, tìm toạ độ giao điểm của (P) và d.

Lập bảng giá trị của hàm số.
Vẽ đồ thị hàm số.
Advertisements (Quảng cáo)
Nhìn đồ thị để kết luận.

a) Đồ thị hàm số y = \(\frac{3}{2}\)x2 là một đường parabol đỉnh O đi qua các điểm A(-2;6), \(B\left( { - 1;\frac{3}{2}} \right)\), O(0;0), \(B’\left( {1;\frac{3}{2}} \right)\), A’(2;6).
Đồ thị hàm số y = 3x là đường thẳng đi qua các điểm O(0;0) và A’(2;6).
Đồ thị của hai hàm số y = \(\frac{3}{2}\)x2 và y = 3x được vẽ như hình dưới.
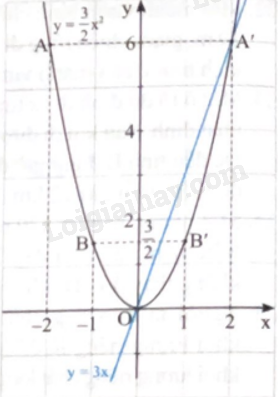
b) Dựa vào hình vẽ, ta có các giao điểm của (P) và d là O(0;0) và A’(2;6).
