Cho mạch điện có sơ đồ như hình 5.6, trong đó điện trở R1=6Ω ;dòng điện mạch chính có cường độ I=1,2A và dòng điện đi qua điện trở R2 có cường độ I2=0,4A.
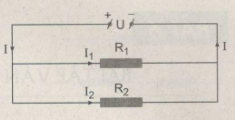
a. Tính R2.
b. Tính hiệu điện thế U đặt vào hai đầu đoạn mạch.
c. Mắc một điện trở R3 vào mạch điện trên , song song với R1 và R2 thì dòng điện trong mạch chính có cường độ là 1,5A. Tính R3 và điện trở tương đương Rtđ của đoạn mạch này khi đó.
a) Mạch gồm \(R_1//R_2\), nên ta có:
+ Hiệu điện thế qua \(R_1\) bằng hiệu điện thế qua \(R_2\) và bằng hiệu điện thế của toàn mạch: \(U=U_1=U_2\)
+ Cường độ dòng điện trong mạch: \(I=I_1+I_2\)
Ta suy ra, cường độ dòng điện qua điện trở \(R_1\) là:
\({I_1} = I - {I_2} = 1,2 - 0,4 = 0,8{\rm{A}}\)
Lại có:
\(I_1=\dfrac{U_1}{R_1}=\dfrac{U}{R_1}=0,8A\) (1)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{U}{R_2}=0,4A\) (2)
Lấy \(\dfrac{(1)}{(2)}\) ta được:
Advertisements (Quảng cáo)
\(\begin{array}{l}\dfrac{{{I_1}}}{{{I_2}}} = \dfrac{{\dfrac{U}{{{R_1}}}}}{{\dfrac{U}{{{R_2}}}}} = \dfrac{{{R_2}}}{{{R_1}}} = \dfrac{{0,8}}{{0,4}} = 2\\ \Rightarrow {R_2} = 2{R_1} = 2.6 = 12\Omega \end{array}\)
b) Ta có: \(U=U_1=U_2\)
Hiệu diện thế qua điện trở \(R_1\) là: \({U_1} = {I_1}.{R_1} = 0,8.6 = 4,8V \)
\(\Rightarrow U = {U_1} = {U_2} = 4,8V\)
Vậy hiệu điện thế đặt vào hai đầu đoạn mạch là: \(U=4,8V\)
c)
Điện trở tương đương của mạch là:
\(R_{tđ} = \dfrac{U}{I} =\dfrac{4,8}{1,5}=3,2\Omega\)
Điện trở tương đương của điện trở \(R_1\) và \(R_2\) là \(R_{12}\)
\({R_{12}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} \)\(=\dfrac{6.12}{6+12}=4\Omega\)
Lại có: \(R_{12}//R_3\)
Ta có:
\(\eqalign{
& {1 \over {{R_{tđ}}}} = {1 \over {{R_3}}} + {1 \over {{R_{12}}}} \cr
& \Rightarrow {1 \over {{R_3}}} = {1 \over {{R_{tđ}}}} - {1 \over {{R_{12}}}} \cr
& \Rightarrow {1 \over {{R_3}}} = {1 \over {3,2}} - {1 \over 4} = {1 \over {16}} \cr
& \Rightarrow {R_3} = 16\Omega \cr} \)
Vậy điện trở \(R_3=16\Omega\) và điện trở tương đương của đoạn mạch là \(R_{tđ}=3,2 \Omega\)
