
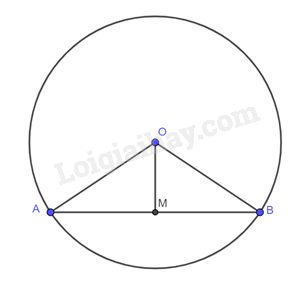
Cho đường tròn \(\left( {O;R} \right)\) và dây \(AB\) khác đường kính. Gọi \(M\) là trung điểm của \(AB\).
a) Đường thẳng \(OM\) có phải là đường trung trực của đoạn thẳng \(AB\) hay không? Vì sao?
b) Tính khoảng cách từ điểm \(O\) đến đường thẳng \(AB\), biết \(R = 5cm,AB = 8cm\).

Dựa vào các kiến thức đã học để giải bài toán.

Advertisements (Quảng cáo)
a) Do \(OA = OB = R\) nên tam giác \(OAB\) cân tại \(O\).
Mà \(M\) là trung điểm của \(AB\) suy ra \(OM\) là đường trung trực của đoạn thẳng \(AB\).
b) Khoảng cách từ điểm \(O\) đến đường thẳng \(AB\) chính là \(OM\).
Do \(M\) là trung điểm của \(AB\) nên \(MA = MB = \frac{{AB}}{2} = 4\left( {cm} \right)\).
Xét tam giác \(OMA\) vuông tại \(M\) có:
\(O{M^2} + M{A^2} = O{A^2}\)(Định lý Pythagore)
\(O{M^2} + {4^2} = {5^2} \Rightarrow OM = 3\left( {cm} \right).\)
Vậy khoảng cách từ điểm \(O\) đến đường thẳng \(AB\) là 3cm.
