Hoạt động3
Trả lời câu hỏi Hoạt động 3 trang 115
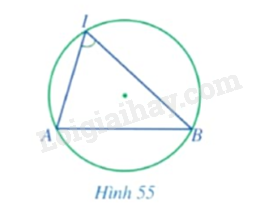
Trong Hình 55, đỉnh của góc \(AIB\) có thuộc đường tròn hay không? Hai cạnh của góc chứa hai dây cung nào của đường tròn?

Dựa vào hình ảnh trực quan để đưa ra nhận xét.

- Đỉnh của góc \(AIB\) có thuộc đường tròn.
- Hai cạnh của góc chứa hai dây cung \(IA,IB\) của đường tròn.
Luyện tập3
Trả lời câu hỏi Luyện tập 3 trang 115
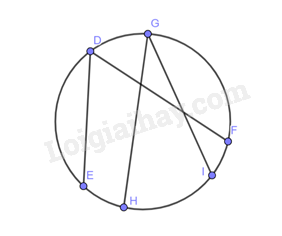
Hãy vẽ một đường tròn và hai góc nội tiếp trong đường tròn đó.

Dựa vào kiến thức vừa học để vẽ hình.

Hoạt động4
Trả lời câu hỏi Hoạt động 4 trang 115
Cho góc \(AIB\) nội tiếp đường tròn tâm \(O\) đường kính \(IK\) sao cho tâm \(O\) nằm trong góc đó (Hình 57).
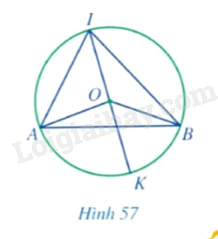
a) Các cặp góc \(\widehat {OAI}\) và \(\widehat {OIA};\widehat {OBI}\) và \(\widehat {OIB}\) có bằng nhau hay không?
b) Tính các tổng \(\widehat {AOI} + 2\widehat {OIA},\widehat {BOI} + 2\widehat {OIB}\).
c) Tính các tổng \(\widehat {AOI} + \widehat {AOK},\widehat {BOI} + \widehat {BOK}\).
d) So sánh \(\widehat {AOK}\) và \(2\widehat {OIA},\widehat {BOK}\) và \(2\widehat {OIB},\widehat {AOB}\) và \(2\widehat {AIB}\).

Dựa vào các kiến thức đã học về đường tròn để xác định.

a) Do \(OI = OA = R\) nên tam giác \(IOA\) cân tại \(O\) suy ra \(\widehat {OAI} = \widehat {OIA}\)
Do \(OI = OB = R\) nên tam giác \(IOB\) cân tại \(O\) suy ra \(\widehat {OBI} = \widehat {OIB}\)
b) Xét tam giác \(AOI\) cân tại \(O\) có:
\(\widehat {AOI} + \widehat {OIA} + \widehat {OAI} = 180^\circ \Rightarrow \widehat {AOI} + \widehat {OIA} + \widehat {OIA} = 180^\circ \Rightarrow \widehat {AOI} + 2\widehat {OIA} = 180^\circ \)
Xét tam giác \(BOI\) cân tại \(O\) có:
\(\widehat {BOI} + \widehat {OIB} + \widehat {OBI} = 180^\circ \Rightarrow \widehat {BOI} + \widehat {OIB} + \widehat {OIB} = 180^\circ \Rightarrow \widehat {BOI} + 2\widehat {OIB} = 180^\circ \)
c) Ta có: \(\widehat {AOI} + \widehat {AOK} = 180^\circ \) (hai góc kề bù)
\(\widehat {BOI} + \widehat {BOK} = 180^\circ \) (hai góc kề bù)
d) Do \(\widehat {AOI} + 2\widehat {OIA} = 180^\circ \) lại có \(\widehat {AOI} + \widehat {AOK} = 180^\circ \) nên \(2\widehat {OIA} = \widehat {AOK}\)
Do \(\widehat {BOI} + 2\widehat {OIB} = 180^\circ \) lại có \(\widehat {BOI} + \widehat {BOK} = 180^\circ \) nên \(2\widehat {OIB} = \widehat {BOK}\)
Ta có: \(\widehat {OIA} + \widehat {OIB} = \widehat {AIB} \Rightarrow 2\left( {\widehat {OIA} + \widehat {OIB}} \right) = 2\widehat {AIB} \Rightarrow 2\widehat {OIA} + 2\widehat {OIB} = 2\widehat {AIB}\)
Advertisements (Quảng cáo)
Mà \(2\widehat {OIA} = \widehat {AOK},2\widehat {OIB} = \widehat {BOK}\) nên \(\widehat {AOK} + \widehat {BOK} = 2\widehat {AIB} \Rightarrow \widehat {AOB} = 2\widehat {AIB}\)
Luyện tập4
Trả lời câu hỏi Luyện tập 4 trang 116
Cho đường tròn \(\left( {O;R} \right)\) và dây cung \(AB = R\). Điểm \(C\) thuộc cung lớn \(AB,C\) khác \(A\) và \(B\). Tính số đo góc \(ACB\).

Dựa vào kiến thức vừa học về góc nội tiếp và góc ở tâm để tính.

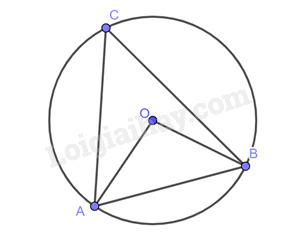
Xét tam giác \(OAB\) có: \(OA = OB = AB = R\).
Suy ra tam giác \(OAB\) là tam giác đều nên \(\widehat {AOB} = 60^\circ \).
Xét đường tròn \(\left( O \right)\): Vì \(\widehat {AOB}\) là góc ở tâm và \(\widehat {ACB}\) là góc nội tiếp cùng chắn cung \(AB\) nên:
\(\widehat {ACB} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}.60^\circ = 120^\circ \).
Vậy \(\widehat {ACB} = 120^\circ \).
Hoạt động5
Trả lời câu hỏi Hoạt động 5 trang 116
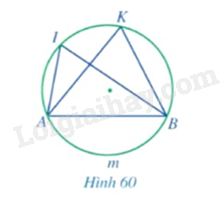
Quan sát Hình 60 và nêu mối liên hệ giữa
a) \(\widehat {AIB}\) và sđ$\overset\frown{AmB}$;
b) \(\widehat {AKB}\) và sđ$\overset\frown{AmB}$;
c) \(\widehat {AIB}\) và \(\widehat {AKB}\).

Dựa vào kiến thức “Góc nội tiếp có số đo bằng nửa số đo cung bị chắn” để làm bài.

a) Ta thấy: \(\widehat {AIB}\) là góc nội tiếp chắn $\overset\frown{AmB}$ nên $\widehat{AIB}=\frac{1}{2}sđ\overset\frown{AmB}$.
b) Ta thấy: \(\widehat {AKB}\) là góc nội tiếp chắn $\overset\frown{AmB}$ nên $\widehat{AKB}=\frac{1}{2}sđ\overset\frown{AmB}$.
c) Do $\widehat{AIB}=\frac{1}{2}sđ\overset\frown{AmB};\widehat{AKB}=\frac{1}{2}sđ\overset\frown{AmB}$ nên \(\widehat {AIB} = \widehat {AKB}\).
Luyện tập5
Trả lời câu hỏi Luyện tập 5 trang 119
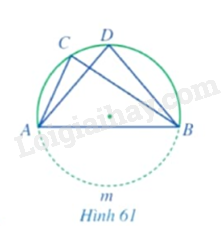
Trong Hình 61, gọi \(I\) là giao điểm của \(AD\) và \(BC\). Chứng minh \(IA.ID = IB.IC\).

Dựa vào tính chất góc nội tiếp để chứng minh.

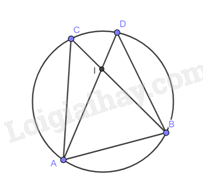
Ta có: \(\widehat {ACB}\) và \(\widehat {ADB}\) là hai góc nội tiếp chắn cung \(AB\) nên \(\widehat {ACB} = \widehat {ADB}\) hay \(\widehat {ACI} = \widehat {BDI}\).
Do \(\widehat {CIA}\) và \(\widehat {DIB}\) là hai góc đối đỉnh nên \(\widehat {CIA} = \widehat {DIB}\).
Xét \(\Delta CIA\) và \(\Delta DIB\) có:
$\left\{ \begin{align}\widehat{ACI}=\widehat{BDI} \\ \widehat{CIA}=\widehat{DIB} \end{align} \right.\Rightarrow \Delta CIA\backsim \Delta DIB\left( g.g \right) \Rightarrow \frac{CI}{DI}=\frac{IA}{IB}\Rightarrow IA.ID=IC.IB.$
