Bài tập 2 trang 69 Toán 9 tập 2 - Chân trời sáng tạo: Cho tam giác ABC ( AC < Bnội tiếp đường tròn (O) có AB là đường kính...

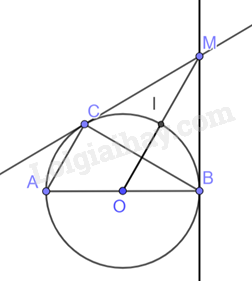
Cho tam giác ABC ( AC < BC) nội tiếp đường tròn (O) có AB là đường kính. Từ điểm O vẽ đường thẳng song song với AC và cắt đường tròn (O) tại I (điểm I thuộc cung nhỏ CB).

a) Chứng minh OI vuông góc với BC.

b) Vẽ tiếp tuyến của đường tròn (O) tại B và cắt OI tại M. Chứng minh MC là tiếp tuyến của đường tròn (O).

- Đọc kỹ dữ kiện đề bài để vẽ hình.

- Chứng minh tam giác ABC vuông tại C và OI // AC để suy ra OI vuông góc với BC.

- Chứng minh \(\Delta \)COM = \(\Delta \)BOM (c – g – c) nên \(\widehat {OBM} = \widehat {OCM} = {90^o}\)

Suy ra MC là tiếp tuyến đường tròn (O).

a) Xét đường tròn (O) có:

\(\widehat {ACB}\) là góc nội tiếp chắn cung AB, mà AB là đường kính của đường tròn (O).

\(\widehat {ACB}\) = 90^o hay tam giác ABC vuông tại C, mà OI // AC (giả thiết).

Suy ra OI \( \bot \) BC (quan hệ từ vuông góc – song song).

b) Vì OB = OC = R suy ra tam giác OBC cân tại O mà OI là đường cao của tam giác OBC.

Suy ra OI đồng thời là phân giác của tam giác OBC.

Suy ra \(\widehat {COI} = \widehat {BOI}\) hay \(\widehat {COM} = \widehat {BOM}\)

Xét \(\Delta \) COM và \(\Delta \) BOM có:

OC = OB = R;

\(\widehat {COM} = \widehat {BOM}\) (chứng minh trên);

OM chung.

Suy ra \(\Delta \)COM = \(\Delta \)BOM (c – g – c).

Do đó, \(\widehat {OBM} = \widehat {OCM}\) (hai góc tương ứng)

Mà \(\widehat {OBM}\) = 90^o (do MB là tiếp tuyến của đường tròn).

Suy ra \(\widehat {OCM}\) = 90^o hay OM \( \bot \) MC mà C thuộc đường tròn (O)

Suy ra MC là tiếp tuyến đường tròn (O).