Câu hỏi/bài tập:

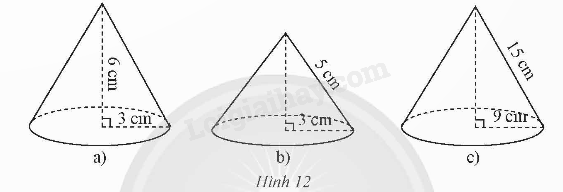
Hãy cho biết chiều cao, bán kính đáy, độ dài đường sinh và diện tích xung quanh của mỗi hình nón sau:

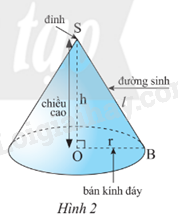
- Dựa vào: Khi quay một tam giác vuông SOB một vòng quanh cạnh góc vuông SO cố định ta được một hình nón.
+ S gọi là đỉnh của hình nón
+ Cạnh OB quét thành hình tròn gọi là đấy của hình nón. Bán kính của đáy gọi là bán kính đáy của hình nón.
+ Cạnh SB quét thành mặt xung quanh của hình nón. Mỗi vị trí của SB là một đường sinh.
+ Độ dài SO là chiều cao hình nón.
- Dựa vào diện tích xung quanh của hình nón có bán kính r, độ dài đường sinh l là: \({S_{xq}} = \pi rl\)

Advertisements (Quảng cáo)
a) Chiều cao h = 6 cm; bán kính đáy r = 3 cm.
Đường sinh là: \(\sqrt {{6^2} + {3^2}} = 3\sqrt 5 \) (cm).
Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi rl = \pi .3.3\sqrt 5 = 9\pi \sqrt 5 \) (cm2).
b) Chiều cao h = \(\sqrt {{h^2} - {r^2}} = \sqrt {{5^2} - {3^2}} \) = 4 cm; bán kính đáy r = 3 cm.
Đường sinh là: l = 5cm.
Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi rl = \pi .3.5 = 15\pi \) (cm2).
c) Chiều cao h = \(\sqrt {{h^2} - {r^2}} = \sqrt {{{15}^2} - {9^2}} \) = 12 cm; bán kính đáy r = 9 cm.
Đường sinh là: l = 15cm.
Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi rl = \pi .9.15 = 135\pi \) (cm2).
