Câu hỏi/bài tập:

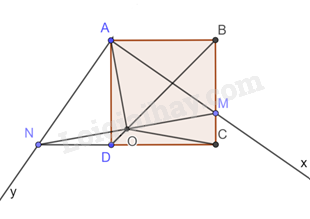
Cho hình vuông ABCD có độ dài cạnh bằng a. Góc vuông xAy thay đổi sao cho tia Ax cắt đoạn thẳng BC tại M và tia Ay cắt đoạn thẳng CD kéo dài tại N.
a) Chứng minh hai tam giác ABM và ADN bằng nhau.
b) Gọi O là trung điểm của MN. Chứng minh ABMO và ANDO là các tứ giác nội tiếp.
c) Chứng minh ba điểm B, D, O thẳng hàng.

- Đọc kỹ dữ liệu để vẽ hình.
- Chứng minh \(\Delta \)ABM = \(\Delta \)ADN (g.c.g)
- Dựa vào trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180o để suy ra tứ giác ABMO và ANDO nội tiếp.
- Chứng minh O là tâm đường tròn ngoại tiếp tứ giác AMCN. Suy ra
OA = OC. Sau đó chứng minh B, D, O cùng thuộc trung trực của đoạn thẳng AC. Vậy ba điểm B, D, O thẳng hàng.

a) Xét \(\Delta \)ABM và \(\Delta \)ADN ta có:
AB = AD
\(\widehat {ABM} = \widehat {ADN}( = {90^o})\)
Advertisements (Quảng cáo)
\(\widehat {BAM} = \widehat {NAD}\)(cùng phụ với \(\widehat {DAM}\))
Do đó \(\Delta \)ABM = \(\Delta \)ADN (g.c.g)
b) Ta có AM = AN (do \(\Delta \)ABM = \(\Delta \)ADN)
Suy ra \(\Delta \) AMN cân tại A
Mà AO cũng là đường trung tuyến (O là trung điểm của NM)
Nên AO cũng là đường cao suy ra AO \( \bot \) NM tại O.
Xét tứ giác ABMO có \(\widehat {ABM} + \widehat {AOM} = {90^o} + {90^o} = {180^o}\) nên tứ giác ABMO nội tiếp.
Xét tứ giác ADNO có \(\widehat {ADN} = {90^o}\left( {AD \bot CN} \right),\widehat {AON} = {90^o}(AO \bot MN)\)
Suy ra D, O thuộc đường tròn đường kính AN.
Vậy tứ giác ADNO nội tiếp.
c) Tứ giác AMCN có: \(\widehat {MAN} + \widehat {MCN} = {90^o} + {90^o} = {180^o}\) nên nội tiếp.
Mà \(\widehat {MAN} = {90^o}\)
Do đó O là tâm đường tròn ngoại tiếp tứ giác AMCN.
Suy ra OA = OC
Mà DA = DC, BA = BC (tứ giác ABCD là hình vuông).
Do đó B, D, O cùng thuộc trung trực của đoạn thẳng AC.
Vậy ba điểm B, D, O thẳng hàng.
