Ta có: \(HB = 1,5m\) Tam giác NHB vuông tại H nên \(NH = NB.\cot HNB\) b) Tam giác AHN vuông tại H nên \(AH = NH.\tan HNA\). Phân tích và giải bài tập 4.12 trang 87 SGK Toán 9 tập 1 - Cùng khám phá Bài 2. Một số hệ thức về cạnh và góc của tam giác vuông. Quan sát Hình 4.27 và tính: a) Khoảng cách NH giữa Nam và cây;b) Chiều cao AB của cây...

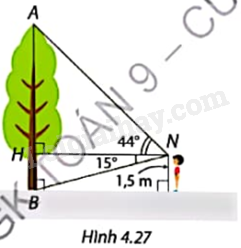
Quan sát Hình 4.27 và tính:
a) Khoảng cách NH giữa Nam và cây;
b) Chiều cao AB của cây.

a) Ta có: \(HB = 1,5m\)
Tam giác NHB vuông tại H nên \(NH = NB.\cot HNB\)
b) Tam giác AHN vuông tại H nên \(AH = NH.\tan HNA\).
Advertisements (Quảng cáo)
Do đó, \(AB = HB + HA\)

a) Ta có: \(HB = 1,5m\).
Tam giác NHB vuông tại H nên
\(NH = NB.\cot HNB = 1,5.\cot {15^o} \approx 5,6\left( m \right)\).
b) Tam giác AHN vuông tại H nên
\(AH = NH.\tan HNA \approx 5,6.\tan {44^o} \approx 5,4\left( m \right)\).
Do đó, \(AB = HB + HA \approx 1,5 + 5,4 \approx 6,9\left( m \right)\).
