
Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho.
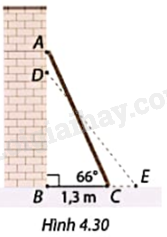
Một chiếc thang AC được dựng vào một bức tường thẳng đứng (Hình 4.30).
a) Ban đầu, khoảng cách từ chân thang đến tường là \(BC = 1,3m\) và góc tạo bởi thang và phương nằm ngang là \(\widehat {ACB} = {66^o}\), tính độ dài của thang.
b) Nếu đầu A của thang bị trượt xuống 40cm đến vị trí D thì góc DEB tạo bởi thang và phương nằm ngang khi đó bằng bao nhiêu?

a) Tam giác ABC vuông tại B nên \(BC = AC.\cos ACB\), từ đó tính được AC.
b)
+ Tam giác ABC vuông tại B nên \(AB = BC.\tan ACB\). Do đó, \(BD = AB - AD\).
+ Ta có: \(AC = DE\).
+ Tam giác BDE vuông tại B nên \(\sin E = \frac{{BD}}{{DE}}\), do đó tính được góc E.
Advertisements (Quảng cáo)

a) Tam giác ABC vuông tại B nên
\(BC = AC.\cos ACB\), suy ra:
\(AC = \frac{{BC}}{{\cos ACB}} = \frac{{1,3}}{{\cos {{66}^o}}} \approx 3,2\left( m \right)\).
Vậy độ dài chiếc thang khoảng 3,2m.
b) Tam giác ABC vuông tại B nên
\(AB = BC.\tan ACB = 1,3.\tan {66^o} \approx 2,9\left( m \right)\).
Do đó, \(BD = AB - AD \approx 2,9 - 0,4 \approx 2,5\left( m \right)\).
Ta có: \(AC = DE \approx 3,2m\).
Tam giác BDE vuông tại B nên
\(\sin E = \frac{{BD}}{{DE}} \approx \frac{{2,5}}{{3,2}}\), do đó \(\widehat E \approx {51^o}23’\).
