
Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho.
Tính số đo góc \(\alpha \) và các độ dài x, y trong mỗi trường hợp ở Hình 4.31.
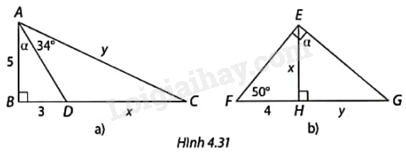

Hình a:
+ Tam giác ABD vuông tại B nên \(\tan \alpha = \tan BAD = \frac{{BD}}{{AB}} = \frac{3}{5}\), tính được góc \(\alpha \).
+ \(\widehat {BAC} = \widehat {BAD} + \widehat {DAC}\).
+ Tam giác ABC vuông tại B nên \(BC = AB.\tan BAC\), \(AB = AC.\cos BAC\) nên tính được y.
+ Ta có: \(x = BC - BD\).
Hình b:
+ Tam giác EHF vuông tại H nên \(x = EH = FH.\tan F\), \(\widehat {FEH} = {90^o} - \widehat F\). Do đó, \(\alpha = \widehat {HEG} = {90^o} - \widehat {FEH}\).
+ Tam giác EHG vuông tại H nên \(y = HG = EH.\tan HEG\).

Hình a:
Advertisements (Quảng cáo)
Tam giác ABD vuông tại B nên
\(\tan \alpha = \tan BAD = \frac{{BD}}{{AB}} = \frac{3}{5}\), suy ra \(\alpha \approx {30^o}58’\).
Do đó, \(\widehat {BAC} = \widehat {BAD} + \widehat {DAC} \approx {64^o}58’\).
Tam giác ABC vuông tại B nên
\(BC = AB.\tan BAC \approx 5.\tan {64^o}58′ \approx 10,7\)
\(AB = AC.\cos BAC\) nên
\(y = AC = \frac{{AB}}{{\cos BAC}} \approx \frac{5}{{\cos {{64}^o}58′}} \approx 11,8\).
Ta có: \(x = BC - BD \approx 10,7 - 3 \approx 7,7\)
Hình b:
Tam giác EHF vuông tại H nên
\(x = EH = FH.\tan F = 4.\tan {50^o} \approx 4,8\), \(\widehat {FEH} = {90^o} - \widehat F = {40^o}\)
Do đó, \(\alpha = \widehat {HEG} = {90^o} - \widehat {FEH} = {50^o}\)
Tam giác EHG vuông tại H nên
\(y = HG = EH.\tan HEG \approx 4,8.\tan {50^o} \approx 5,7\)
