Bài 4.8 trang 86 Toán 9 Cùng khám phá tập 1: Tính độ dài cạnh x, y và số đo góc $\alpha$ trong mỗi trường hợp ở Hình 4...

Tính độ dài cạnh x, y và số đo góc $\alpha$ trong mỗi trường hợp ở Hình 4.23.

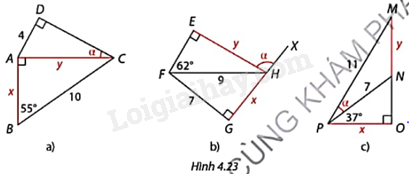
Hình a: $\Delta$ABC vuông tại A nên $y = BC.\sin B;x = BC.\cos B$

$\Delta$ADC vuông tại D nên $\sin \alpha = \frac{{AD}}{{AC}}$ nên tính được $\alpha$.

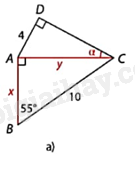
Hình b:

+ $\Delta$GFH vuông tại F nên $F{G^2} + G{H^2} = F{H^2}$ nên tính được x

$\sin GHF = \frac{{FG}}{{FH}} = \frac{7}{9}$ nên tính được góc FHG.

+ $\Delta$EFH vuông tại E nên $y = FH.\sin EFH,\widehat {EHF} = {90^o} - \widehat {EFH}$. Do đó, $\alpha = {180^o} - \widehat {EHF} - \widehat {FHG}$.

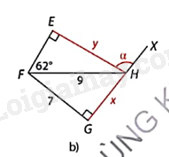
Hình c:

+ $\Delta$ONP vuông tại O nên $x = PN.\cos NPO,NO = PN.\sin NPO$

+ $\Delta$OMP vuông tại O nên $\cos OPM = \frac{{OP}}{{PM}}$ nên tính được góc OPM, $MO = PM.\sin MPO$

Do đó, $\alpha = \widehat {OPM} - \widehat {OPN},y = MN = MO - NO$

Hình a:

$\Delta$ABC vuông tại A nên

$y = BC.\sin B = 10\sin {55^o} \approx 8,2;x = BC.\cos B = 10\cos {55^o} \approx 5,7$

Tam giác ADC vuông tại D nên

$\sin \alpha = \frac{{AD}}{{AC}} = \frac{4}{{8,2}} = \frac{{20}}{{41}}$ nên $\alpha \approx {29^o}12’$.

Hình b:

$\Delta$GFH vuông tại F nên $F{G^2} + G{H^2} = F{H^2}$ (định lí Pythagore) nên $x = GH = \sqrt {F{H^2} - F{G^2}} = \sqrt {{9^2} - {7^2}} = 4\sqrt 2 \approx 5,7$

$\sin GHF = \frac{{FG}}{{FH}} = \frac{7}{9}$ nên $\widehat {FHG} \approx {51^o}3’$

$\Delta$EFH vuông tại E nên

$y = FH.\sin EFH = 9.\sin {62^o} \approx 7,9$, $\widehat {EHF} = {90^o} - \widehat {EFH} = {90^o} - {62^o} = {28^o}$.

Do đó, $\alpha = {180^o} - \widehat {EHF} - \widehat {FHG}$ $\approx {180^o} - {28^o} - {29^o}11’$ $\approx {122^o}49’$.

Hình c:

$\Delta$ONP vuông tại O nên $x = PN.\cos NPO = 7.\cos {37^o} \approx 5,6$, $NO = PN.\sin NPO = 7.\sin {37^o} \approx 4,2$.

$\Delta$OMP vuông tại O nên $\cos OPM = \frac{{OP}}{{PM}} \approx \frac{{5,6}}{{11}}$ nên $\widehat {OPM} \approx {59^o}24’$,

$MO = PM.\sin MPO = 11.\sin {59^o}24′ \approx 9,5$

Do đó, $\alpha = \widehat {OPM} - \widehat {OPN} \approx {22^o}24′,y = MN = MO - NO \approx 5,3$