Giải mục 2 trang 84, 85 Toán 9 Cùng khám phá tập 1: Trong mỗi trường hợp dưới đây, hãy xác định độ dài các cạnh và số đo góc ở các ô...

Hoạt động2

Trả lời câu hỏi Hoạt động 2 trang 84

Trong mỗi trường hợp dưới đây, hãy xác định độ dài các cạnh và số đo góc ở các ô . Làm tròn số đo góc đến độ và độ dài cạnh đến hàng phần mười. Cho biết em đã sử dụng hệ thức, định lí nào để tính.

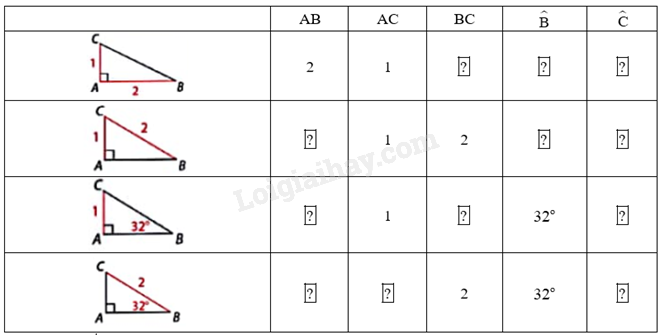
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:

+ Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề;

+ Cạnh góc vuông còn lại nhân tang góc đối hoặc côtang góc kề.

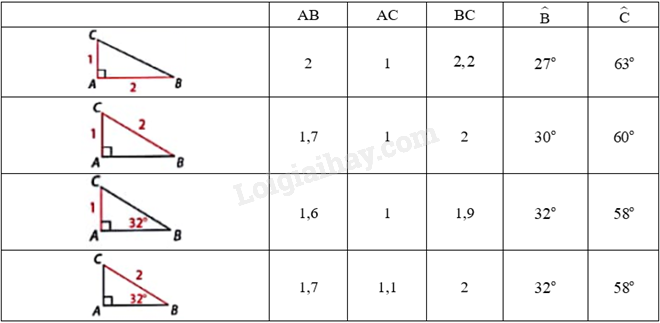
Em đã sử dụng các kiến thức:

- Trong một tam giác vuông, mỗi cạnh góc vuông bằng:

+ Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề;

+ Cạnh góc vuông còn lại nhân tang góc đối hoặc côtang góc kề.

- Sử dụng định lí Pythagore trong tam giác vuông.

- Trong tam giác vuông có góc nhọn $\alpha$, khi đó:

+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là $\sin \alpha$.

+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là $\cos \alpha$.

+ Tỉ số giữa cạnh đối và cạnh kề được gọi là $\tan \alpha$.

+ Tỉ số giữa cạnh kề và cạnh đối được gọi là $\cot \alpha$.

Luyện tập2

Trả lời câu hỏi Luyện tập 2 trang 85

Giải các tam giác vuông MNP và XYZ trong Hình 4.21. Làm tròn số đo góc đến độ và độ dài cạnh đến hàng phần mười.

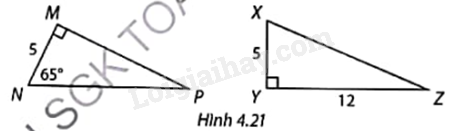
Tam giác MNP vuông tại M nên $\hat P = {90^o} - \hat N$, $MP = MN.\tan N$, $NP = \frac{{NM}}{{\cos N}}$.

Tam giác XYZ vuông tại Y nên $XZ = \sqrt {X{Y^2} + Y{Z^2}}$, $\cos X = \frac{{XY}}{{XZ}}$ nên tính được góc X, $\widehat Z = {90^o} - \widehat X$.

Tam giác MNP vuông tại M nên:

$\widehat P = {90^o} - \widehat N = {90^o} - {65^o} = {25^o}$.

$\begin{array}{l}MP = MN.\tan N = 5.\tan {65^o} \approx 10,7\\NP = \frac{{NM}}{{\cos N}} = \frac{5}{{\cos {{65}^o}}} = 11,8\end{array}$

Tam giác XYZ vuông tại Y nên:

$XZ = \sqrt {X{Y^2} + Y{Z^2}} = \sqrt {{5^2} + {{12}^2}} = 13$

$\cos X = \frac{{XY}}{{XZ}} = \frac{5}{{13}}$ nên $\widehat X \approx {67^o}$.

Suy ra: $\widehat Z = {90^o} - \widehat X \approx {23^o}$.

Vận dụng2

Trả lời câu hỏi Vận dụng 2 trang 85 SGK Toán 9

Trong Hình 4.22, một người đứng từ sân thượng tòa nhà và quan sát một người đi xe máy từ vị trí C đến vị trí D.

a) Giải tam giác vuông ABD.

b) Tính tốc độ của xe máy, biết thời gian xe đi từ C đến D là 6,5 giây. Làm tròn số đo góc đến độ và độ dài cạnh đến hàng phần mười mét.

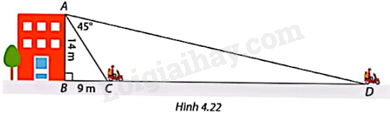
a) + Tam giác ABC vuông tại B nên $\tan BAC = \frac{{BC}}{{AB}}$, từ đó tính được góc BAC.

+ $\widehat {BAD} = \widehat {BAC} + \widehat {CAD}$, $\widehat D = {90^o} - \widehat {BAD}$.

+ $AD = \frac{{AB}}{{\sin D}},BD = \frac{{AB}}{{\tan D}}$.

b) Áp dụng công thức: $v = \frac{s}{t}$, trong đó s là quãng đường CD và t thời gian xe đi từ C đến D là 6,5 giây.

a) Tam giác ABC vuông tại B nên $\tan BAC = \frac{{BC}}{{AB}} = \frac{9}{{14}}$ nên $\widehat {BAC} \approx {33^o}$.

Suy ra: $\widehat {BAD} = \widehat {BAC} + \widehat {CAD} \approx {78^o}$

Tam giác ABD vuông tại B nên $\widehat D = {90^o} - \widehat {BAD} \approx {12^o}$.

$\begin{array}{l}AD = \frac{{AB}}{{\sin D}} \approx \frac{{14}}{{\sin {{12}^o}}} \approx 67,3\left( m \right),\\BD = \frac{{AB}}{{\tan D}} \approx \frac{{14}}{{\tan {{12}^o}}} \approx 65,9\left( m \right)\end{array}$

b) $CD = BD - BC = 65,9 - 9 = 56,9\left( m \right)$.

Tốc độ của xe máy đi từ C đến D là:

$\frac{{56,9}}{{6,5}} \approx 8,8\left( {m/s} \right)$.