Kẻ DK vuông góc với BC tại K. + Tam giác AHB vuông tại H nên \(AH = AB.\sin B\). Phân tích và giải bài tập 4.9 trang 86 SGK Toán 9 tập 1 - Cùng khám phá Bài 2. Một số hệ thức về cạnh và góc của tam giác vuông. Tính độ dài cạnh bên CD của hình thang ABCD trong Hình 4.24...

Tính độ dài cạnh bên CD của hình thang ABCD trong Hình 4.24.
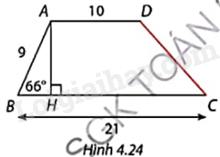

+ Kẻ DK vuông góc với BC tại K.
+ Tam giác AHB vuông tại H nên \(AH = AB.\sin B\).
+ Chứng minh tứ giác AHKD là hình bình hành. Do đó, \(HK = AD = 10,DK = AH\).
+ Áp dụng định lí Pythagore vào tam giác DKC vuông tại K để tính CD.
Advertisements (Quảng cáo)

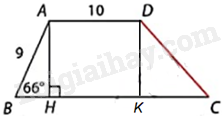
Kẻ DK vuông góc với BC tại K.
\(\Delta \)AHB vuông tại H nên
\(AH = AB.\sin B = 9.\sin {66^o} \approx 8,2\)
Tứ giác AHKD có: AD//HK (gt), AH//DK (cùng vuông góc với BC) nên tứ giác AHKD là hình bình hành. Do đó, \(HK = AD = 10,DK = AH \approx 8,2\).
\(\Delta \)DKC vuông tại K nên
\(D{C^2} = D{K^2} + K{C^2} \approx 8,{2^2} + {10^2} \approx 167,24\) (Định lí Pythagore) nên \(DC \approx 12,9\).
