
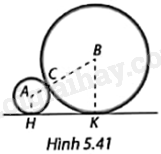
Hình 5.41 cho thấy mặt cắt của hai ống nước nhựa được đặt sát nhau trên mặt đất. Ống nhỏ có đường kính 6cm, ống lớn có đường kính 18cm. Tính:
a) Khoảng cách AB giữa tâm của hai mặt cắt;
b) Khoảng cách HK giữa hai tiếp điểm của mặt cắt hai ống với mặt đất.

a) Cho hai đường tròn phân biệt (O; R) và (O’; r) và \(d = OO’\). Nếu \(d = R + r\) thì hai đường tròn tiếp xúc ngoài.
b) + Qua C kẻ đường thẳng vuông góc với AB, cắt HK tại E.
+ Suy ra CE là tiếp tuyến của đường tròn (A) và CE là tiếp tuyến của đường tròn (B).
+ Sử dụng tính chất hai tiếp tuyến cắt nhau suy ra:
\(CE = EH,\widehat {CEA} = \widehat {AEH} = \frac{1}{2}\widehat {HEC}\), \(CE = EK,\widehat {CEB} = \widehat {BEK} = \frac{1}{2}\widehat {KEC}\).
+ Chứng minh \(HK = EH + EK = 2CE\)
+ Chứng minh \(\widehat {AEB} = {90^o}\).
+ Chứng minh \(\Delta ACE\backsim \Delta ECB\left( g.g \right)\), \(E{C^2} = AC.CB\), tính được EC.
Advertisements (Quảng cáo)

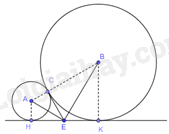
a) Bán kính đường tròn nhỏ là: \(AC = AH = \frac{6}{2} = 3cm\), bán kính đường tròn lớn là: \(BC = BK = \frac{{18}}{2} = 9cm\)
Vì hai đường tròn (A) và (B) tiếp xúc ngoài tại C nên \(AB = AC + CB = 3 + 9 = 12\left( {cm} \right)\)
b) Qua C kẻ đường thẳng vuông góc với AB, cắt HK tại E.
Do đó, CE là tiếp tuyến của đường tròn (A) và CE là tiếp tuyến của đường tròn (B).
Vì CE và HE là tiếp tuyến của đường tròn (A) nên \(CE = EH,\widehat {CEA} = \widehat {AEH} = \frac{1}{2}\widehat {HEC}\).
Vì CE và EK là tiếp tuyến của đường tròn (B) nên \(CE = EK,\widehat {CEB} = \widehat {BEK} = \frac{1}{2}\widehat {KEC}\).
Do đó, \(HK = EH + EK = 2CE\).
Ta có: \(\widehat {HEC} + \widehat {CEK} = {180^o}\), nên \(\frac{1}{2}\left( {\widehat {HEC} + \widehat {CEK}} \right) = {90^0}\), suy ra \(\widehat {AEC} + \widehat {CEB} = {90^o}\) hay \(\widehat {AEB} = {90^o}\).
Tam giác ACE và tam giác ECB có: \(\widehat {ECA} = \widehat {ECB} = {90^o},\widehat {CAE} = \widehat {CEB}\) (cùng phụ với góc AEC).
Do đó, \(\Delta ACE\backsim \Delta ECB\left( g.g \right)\), suy ra \(\frac{{CE}}{{CB}} = \frac{{AC}}{{EC}}\), suy ra \(E{C^2} = AC.CB = 3.9 = 27\), suy ra \(EC = 3\sqrt 3 cm\).
Vậy \(HK = 2CE = 6\sqrt 3 cm\).
