
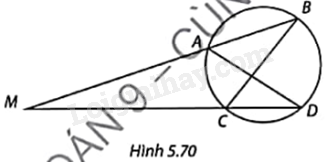
Trong Hình 5.70, hai cát tuyến AB và CD của đường tròn cắt nhau tại M.
a) Chứng minh rằng $\Delta AMD\backsim \Delta CMB$.
b) Tính MB và MC, biết \(MD = 100,MA = 70,AD = 40,BC = 42\).

a) + Vì góc MDA và góc MBC là góc nội tiếp cùng chắn cung AC nên \(\widehat {MDA} = \widehat {MBC}\).
+ Chứng minh $\Delta AMD\backsim \Delta CMB\left( g.g \right)$.
b) + Vì $\Delta AMD\backsim \Delta CMB$ nên \(\frac{{MA}}{{MC}} = \frac{{MD}}{{MB}} = \frac{{AD}}{{CB}}\), suy ra \(\frac{{70}}{{MC}} = \frac{{100}}{{MB}} = \frac{{40}}{{42}} = \frac{{20}}{{21}}\), từ đó tính MC, MB.
Advertisements (Quảng cáo)

a) Vì góc MDA và góc MBC là góc nội tiếp cùng chắn cung AC nên \(\widehat {MDA} = \widehat {MBC}\).
Tam giác AMD và tam giác CMB có:
\(\widehat {MDA} = \widehat {MBC}\),
góc M chung.
Do đó, $\Delta AMD\backsim \Delta CMB\left( g.g \right)$.
b) Vì $\Delta AMD\backsim \Delta CMB$ nên \(\frac{{MA}}{{MC}} = \frac{{MD}}{{MB}} = \frac{{AD}}{{CB}}\), suy ra \(\frac{{70}}{{MC}} = \frac{{100}}{{MB}} = \frac{{40}}{{42}} = \frac{{20}}{{21}}\).
Do đó, \(MC = 70:\frac{{20}}{{21}} = \frac{{147}}{2}\), \(MB = 100:\frac{{20}}{{21}} = 105\).
