Bài 5.33 trang 127 Toán 9 Cùng khám phá tập 1: Tính số đo x trong mỗi trường hợp ở Hình 5...

Tính số đo x trong mỗi trường hợp ở Hình 5.72.

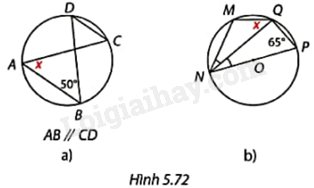
a) + Vì góc DCA và góc DBA là các góc nội tiếp cùng chắn cung nhỏ AD nên $\widehat {DCA} = \widehat {DBA}$.

Vì AB//CD nên $x = \widehat {DCA}$.

b) + Vì góc QPN là góc nội tiếp chắn cung nhỏ NQ nên: $sđ{{\overset\frown{QN}}_{nhỏ}}=2\widehat{NPQ}$

+ $sđ{{\overset\frown{QN}}_{nhỏ}}+sđ{{\overset\frown{PQ}}_{nhỏ}}={{180}^{o}}$ nên tính được số đo cung PQ nhỏ.

+ Vì góc MNQ là góc nội tiếp chắn cung nhỏ MQ, góc QNP là góc nội tiếp chắn cung nhỏ PQ của đường tròn (O). Mà $\widehat{MNQ}=\widehat{QNP}$ nên $sđ{{\overset\frown{MQ}}_{nhỏ}}=sđ{{\overset\frown{PQ}}_{nhỏ}}$.

+ $sđ{{\overset\frown{MN}}_{nhỏ}}=sđ{{\overset\frown{QN}}_{nhỏ}}-sđ{{\overset\frown{MQ}}_{nhỏ}}$.

+ Vì góc NQM là góc nội tiếp chắn cung nhỏ NM của (O) nên $x = \frac{1}{2}{.80^o} = {40^o}$.

a) Vì góc DCA và góc DBA là các góc nội tiếp cùng chắn cung AD nên $\widehat {DCA} = \widehat {DBA} = {50^o}$.

Vì AB//CD nên $x = \widehat {DCA} = {50^o}$.

b) Vì góc QPN là góc nội tiếp chắn cung nhỏ NQ nên:

$sđ{{\overset\frown{QN}}_{nhỏ}}=2\widehat{NPQ}={{2.65}^{o}}={{130}^{o}}$.

Ta có: $sđ{{\overset\frown{QN}}_{nhỏ}}+sđ{{\overset\frown{PQ}}_{nhỏ}}={{180}^{o}}$ nên

$sđ{{\overset\frown{PQ}}_{nhỏ}}={{180}^{o}}-sđ{{\overset\frown{QN}}_{nhỏ}}={{180}^{o}}-{{130}^{o}}={{50}^{o}}$.

Vì góc MNQ là góc nội tiếp chắn cung nhỏ MQ, góc QNP là góc nội tiếp chắn cung nhỏ PQ của đường tròn (O). Mà $\widehat{MNQ}=\widehat{QNP}$ nên

$sđ{{\overset\frown{MQ}}_{nhỏ}}=sđ{{\overset\frown{PQ}}_{nhỏ}}={{50}^{o}}$.

Ta có:

$sđ{{\overset\frown{MN}}_{nhỏ}}=sđ{{\overset\frown{QN}}_{nhỏ}}-sđ{{\overset\frown{MQ}}_{nhỏ}}={{130}^{o}}-{{50}^{o}}={{80}^{o}}.$

Vì góc NQM là góc nội tiếp chắn cung nhỏ NM của (O) nên $x = \frac{1}{2}{.80^o} = {40^o}$.