
Cho đường tròn tâm O và AB là một dây không đi qua tâm của (O). Gọi M là trung điểm của đoạn thẳng AB.
a) Chứng minh rằng OM vuông góc với AB.
b) Biết bán kính của đường tròn (O) là 10cm và \(OM = 6cm\), tính độ dài dây AB.

a) Chứng minh tam giác AOB cân tại O nên OM là đường trung tuyến đồng thời là đường cao.
b) Áp dụng định lí Pythagore vào tam giác AMO vuông tại M để tính AM, từ đó tính được AB.
Advertisements (Quảng cáo)

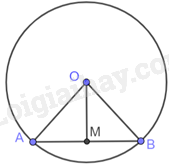
a) Xét (O) có: \(OA = OB\) nên tam giác OAB cân tại O. Do đó, OM là đường trung tuyến đồng thời là đường cao. Suy ra, OM vuông góc với AB.
b) Vì OM vuông góc với AB nên tam giác AOM vuông tại M.
Do đó, \(O{M^2} + A{M^2} = O{A^2}\) (định lí Pythagore),
suy ra \(AM = \sqrt {O{A^2} - O{M^2}} = \sqrt {{{10}^2} - {6^2}} = 8\left( {cm} \right)\)
Vậy \(AB = 2AM = 2.8 = 16\left( {cm} \right)\).
