
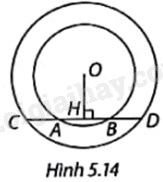
Trong Hình 5.14, cho hai đường tròn cùng tâm O, các điểm A, B, C, D thẳng hàng và \(OH \bot AB\left( {H \in AB} \right)\).
a) Chứng minh rằng H là trung điểm của AB và CD.
b) Chứng minh rằng \(AC = BD\).
c) Biết bán kính đường tròn lớn là 10cm, \(CD = 16cm\) và \(AB = 8cm\). Tính bán kính đường tròn nhỏ.

a) Xét đường tròn (O, OC) có: \(OC = OD\) nên tam giác COD cân tại O. Do đó, OH là đường cao đồng thời là đường trung tuyến. Suy ra, H là trung điểm của CD.
Xét (O, OA) có: \(OA = OB\) nên tam giác OAB cân tại O. Do đó, OH là đường cao đồng thời là đường trung tuyến. Suy ra, H là trung điểm của AB.
b) Theo a ta có: \(CH = HD\), \(AH = HB\) nên \(CH - HA = HD - HB\), suy ra \(AC = BD\).
c) Tam giác HOD vuông tại H nên \(O{H^2} + H{D^2} = O{D^2}\)
Tam giác HOB vuông tại H nên \(O{B^2} = O{H^2} + H{B^2}\), từ đó tính được bán kính đường tròn nhỏ.

Advertisements (Quảng cáo)
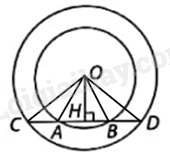
a) Xét đường tròn (O, OC) có: \(OC = OD\) nên tam giác COD cân tại O. Do đó, OH là đường cao đồng thời là đường trung tuyến. Suy ra, H là trung điểm của CD. Do đó, \(CH = HD\).
Xét (O, OA) có: \(OA = OB\) nên tam giác OAB cân tại O. Do đó, OH là đường cao đồng thời là đường trung tuyến. Suy ra, H là trung điểm của AB. Do đó, \(AH = HB\).
b) Theo a ta có: \(CH = HD\), \(AH = HB\) nên \(CH - HA = HD - HB\), suy ra \(AC = BD\).
c) Ta có:
\(\begin{array}{l}HD = \frac{1}{2}CD = \frac{1}{2}.16 = 8\left( {cm} \right),\\HB = \frac{1}{2}AB = \frac{1}{2}.8 = 4\left( {cm} \right)\end{array}\).
Tam giác HOD vuông tại H nên
\(O{H^2} + H{D^2} = O{D^2}\) (định lí Pythagore),
suy ra \(O{H^2}\) \( = O{D^2} - H{D^2}\) \( = {10^2} - {8^2}\) \( = 36\left( {cm} \right)\).
Tam giác HOB vuông tại H nên
\(O{B^2} = O{H^2} + H{B^2} = 36 + {4^2} = 52\) (định lí Pythagore),
suy ra \(OB = 2\sqrt {13} cm\).
