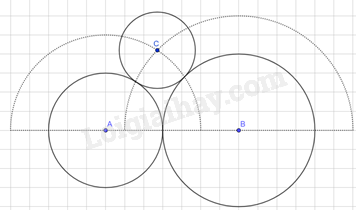
Hoạt động
Trả lời câu hỏi Hoạt động trang 103
Hình 5.16 thể hiện vị trí tương đối khác nhau của hai đường tròn khi đường tròn nhỏ di chuyển từ ngoài vào phía trong đường tròn lớn. Nêu số điểm chung của hai đường tròn trong mỗi trường hợp.
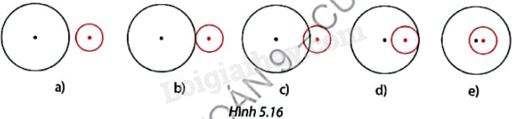

Quan sát hình và nêu số điểm chung của hai đường tròn.

Hình 5.16a: Hai đường tròn không có điểm chung.
Hình 5.16b: Hai đường tròn có 1 điểm chung.
Hình 5.16c: Hai đường tròn có 2 điểm chung.
Hình 5.16d: Hai đường tròn có 1 điểm chung.
Hình 5.16e: Hai đường tròn không có điểm chung.
Luyện tập2
Trả lời câu hỏi Luyện tập 1 trang 104
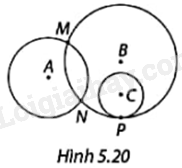
Chỉ ra các cặp đường tròn cắt nhau, tiếp xúc nhau và không giao nhau trong Hình 5.20.

Hai đường tròn được gọi là cắt nhau nếu chúng có đúng 2 điểm chung.
Hai đường tròn được gọi là tiếp xúc nhau nếu chúng có đúng 1 điểm chung.
Hai đường tròn được gọi là không giao nhau nếu chúng không có điểm chung nào.

Đường tròn (A) và đường tròn (B) cắt nhau tại hai giao điểm là A và B.
Hai đường tròn (A) và (C) không giao nhau.
Hai đường tròn (B) và (C) tiếp xúc nhau tại tiếp điểm P.
Luyện tập2
Trả lời câu hỏi Luyện tập 2 trang 105
Cho đường tròn bán kính \(R = 11cm\) và \(r = 7cm\). Xác định vị trí tương đối của hai đường tròn nếu khoảng cách giữa hai tâm bằng:
a) 2cm;
b) 4cm;
c) 21cm;
Advertisements (Quảng cáo)
d) 18cm;
e) 15cm.

Cho hai đường tròn phân biệt (O; R) và (O’; r) và \(d = OO’\). Vị trí tương đối giữa hai đường tròn (O; R) và (O’; r) có thể xác định dựa vào hệ thức liên hệ giữa R, r và d như sau:
+ Nếu \(d > R + r\) thì hai đường tròn ngoài nhau.
+ Nếu \(d = R + r\) thì hai đường tròn tiếp xúc ngoài.
+ Nếu \(R + r > d > R - r\) thì hai đường tròn cắt nhau.
+ Nếu \(d = R - r\) thì hai đường tròn tiếp xúc trong.
+ Nếu \(d < R - r\) thì (O) đựng (O’).

Ta có: \(R - r = 11 - 7 = 4cm\), \(R + r = 11 + 7 = 18cm\).
a) Vì \(R - r = 4cm > 2cm\) nên đường tròn bán kính R đựng đường tròn bán kính r.
b) Vì \(R - r = 4cm\) nên hai đường tròn tiếp xúc trong.
c) Vì \(R + r = 18cm < 21cm\) nên hai đường tròn ngoài nhau.
d) Vì \(R + r = 18cm\) nên hai đường tròn tiếp xúc ngoài.
e) Vì \(R + r > 15cm > R - r\) nên hai đường tròn cắt nhau.
Vận dụng
Trả lời câu hỏi Vận dụng trang 105
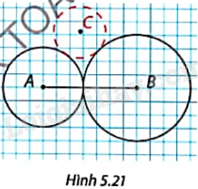
Trong Hình 5.21, hai đường tròn (A; 3) và (B; 4) tiếp xúc ngoài nhau. Sử dụng compa và thước thẳng để dựng đường tròn (C; 2) tiếp xúc ngoài với cả hai đường tròn (A) và (B).

Cho hai đường tròn phân biệt (O; R) và (O’; r) và \(d = OO’\). Nếu \(d = R + r\) thì hai đường tròn tiếp xúc ngoài.

Vì đường tròn (C; 2) tiếp xúc ngoài với cả hai đường tròn (A; 3) và (B; 4) nên
\(\begin{array}{l}CB = 4 + 2 = 6,\\CA = 3 + 2 = 5.\end{array}\)
Vẽ nửa đường tròn (B; 6) và nửa đường tròn (A; 5) (hai nửa đường tròn này nằm cùng phía so với đường thẳng AB).
Gọi C là giao điểm của hai nửa đường tròn (B; 6), (A; 5).
Vẽ đường tròn (C; 2), khi đó ta được đường tròn (C; 2) tiếp xúc ngoài với cả hai đường tròn (A) và (B).