Dựa vào: Nếu \({x_1},{x_2}\) là hai nghiệm của phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) thì. Giải chi tiết bài tập 6.14 trang 18 SGK Toán 9 tập 2 - Cùng khám phá - Bài 3. Định lí Viète và ứng dụng. Với mỗi phương trình ở Bảng 6. 6: a) Tìm các số thích hợp cho mỗi ô ? ở cột \(\Delta \). b) Nếu phương trình có nghiệm \({x_1};{x_2}\), không giải phương trình, hãy tìm các số thích hợp cho mỗi ô ?...

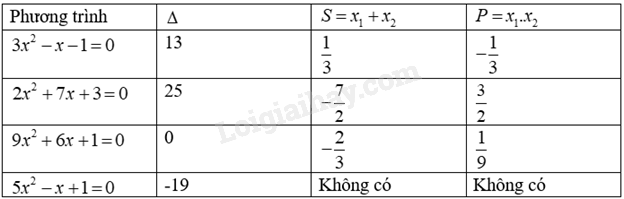
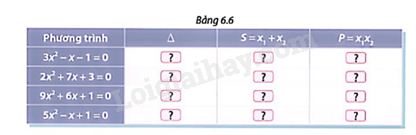
Với mỗi phương trình ở Bảng 6.6:
a) Tìm các số thích hợp cho mỗi ô ? ở cột \(\Delta \).
b) Nếu phương trình có nghiệm \({x_1};{x_2}\), không giải phương trình, hãy tìm các số thích hợp cho mỗi ô ? ở cột S và P.
Advertisements (Quảng cáo)

Dựa vào: Nếu \({x_1},{x_2}\) là hai nghiệm của phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) thì:
\(\left\{ {\begin{array}{*{20}{c}}{S = {x_1} + {x_2} = - \frac{b}{a}}\\{P = {x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)