Cách vẽ đồ thị \(y = a{x^2}\left( {a \ne 0} \right)\) như sau: Vẽ hệ trục toạ độ Oxy. Hướng dẫn giải bài tập 6.2 trang 5 SGK Toán 9 tập 2 - Cùng khám phá - Bài 1. Hàm số y = ax^2 (a khác 0) và đồ thị. Cho hàm số y = - x2. a) Vẽ đồ thị hàm số. b) Tìm trên đồ thị những điểm có tung độ bằng -4...

Cho hàm số y = - x2.
a) Vẽ đồ thị hàm số.
b) Tìm trên đồ thị những điểm có tung độ bằng -4

Cách vẽ đồ thị \(y = a{x^2}\left( {a \ne 0} \right)\) như sau:
Vẽ hệ trục toạ độ Oxy.
Lập bảng một số giá trị tương ứng của x và y. Đánh dấu các điểm tương ứng trên mặt phẳng toạ độ. Ta thường lấy điểm O và những điểm có hoành độ đối nhau.
Advertisements (Quảng cáo)
Vẽ đường thẳng parabol đi qua các điểm vừa đánh dấu.

a) Bảng giá trị tương ứng x và y:

Trên mặt phẳng tọa độ, đánh dấu các điểm A(-2;-4), B(-1;-1), O(0;0), B’(1;-1), A’(2;-4)
Đồ thị hàm số y = -x2 là đường parabol đi qua năm điểm A, B, O, B’, A’.
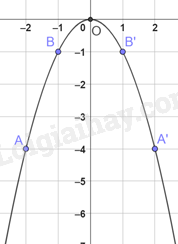
b) Trên đồ thị những điểm có tung độ bằng -4 là A(-2;-4) và A’(2; -4).
