Bài tập 9.12 trang 83 Toán 9 tập 2 - Cùng khám phá: Tính khối lượng thép cần dùng để sản xuất 1000 chiếc đinh tán có thân hình trụ và đầu là...

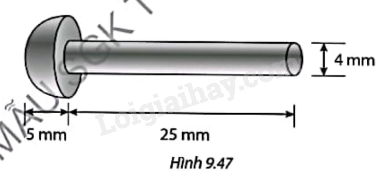
Tính khối lượng thép cần dùng để sản xuất 1000 chiếc đinh tán có thân hình trụ và đầu là nửa hình cầu với kích thước như Hình 9.47, biết khối lượng riêng của thép là 7850 kg/m³.

Thể tích của hình trụ: \(V = \pi {R^2}h\) (với R là bán kính đáy hình trụ, h là chiều cao)

Thể tích của hình cầu là: \(V = \frac{4}{3}\pi {R^3}\)(với R là bán kính hình cầu)

Khối lượng thép: m = V.D (D là khối lượng riêng)

Thể tích phần hình trụ là:

\(V = \pi {R^2}h = \pi {.2^2}.25 = 100\pi \)(mm³)

Thể tích nửa hình cầu là:

\(V = \frac{4}{3}\pi {R^3} = \frac{{16}}{3}\pi \)(mm³)

Thể tích một chiếc đinh tán là:

\(100\pi + \frac{{16}}{3}\pi \approx 105\)(mm³)

Thể tích 1000 chiếc đinh tán là:

105.1000 = 105 000 (mm³) = 0,000105 (m³)

Suy ra khối lượng thép là:

m = D.V = 7850.0,000105 \( \approx \) 0,8 kg.