Chu vi đường tròn: C = \(\pi {r^2}\)(r là bán kính đường tròn). Giải và trình bày phương pháp giải Câu hỏi Hoạt động 2 trang 71 SGK Toán 9 Cùng khám phá - Bài 2. Hình nón.
Câu hỏi/bài tập:
Cắt mặt xung quanh của một hình nón có đường sinh dài 6 cm, bán kính đáy 2 cm (Hình 9.22a) dọc theo đường sinh SA của nó rồi trải phẳng ra, ta được hình khai triển của hình nón đó (Hình 9.22b).
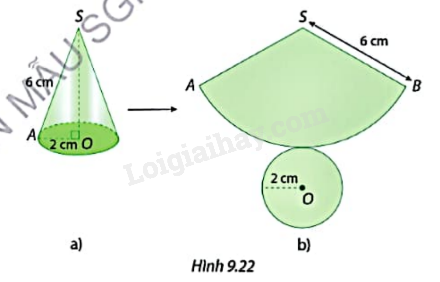
a) Tính chu vi đáy của hình nón, từ đó cho biết độ dài cung ứng với hình quạt tròn ở Hình 9.22b.
b) Tính diện tích của hình quạt tròn khai triển trong Hình 9.22b.

Chu vi đường tròn: C = \(\pi {r^2}\)(r là bán kính đường tròn).
Advertisements (Quảng cáo)

a) Chu vi đáy hình nón là:
\(\pi {r^2} = 4\pi \)(cm).
Suy ra độ dài cung ứng với hình quạt tròn là: \(r.n\) (n: số đo góc ở tâm chắn cung đó).
b) Diện tích hình quạt tròn khai triển là:
S = \(\frac{{\pi .{r^2}.n}}{{360}}\).
