Hoạt động1
Trả lời câu hỏi Hoạt động 1 trang 75
1. Vẽ một góc nhọn có số đo \(\alpha \) bất kì. Chọn một điểm C trên một cạnh và vẽ đường vuông góc CA từ C xuống cạnh còn lại (Hình 4.3). Hãy đo và tính các tỉ số cạnh đối và cạnh huyền, cạnh kề và cạnh huyền, cạnh đối và cạnh kề của góc B trong tam giác ABC.
2. Vẽ thêm một góc nhọn B’ cũng có số đo \(\alpha \) như trên và thực hiện tương tự.
3. Sử dụng dấu hiệu đồng dạng của hai tam giác vuông, hãy giải thích vì sao các cặp tỉ số tương ứng của \(\widehat B\) và \(\widehat {B’}\) bằng nhau.
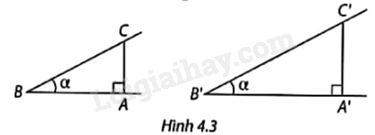

Chứng minh tam giác ABC đồng dạng với tam giác A’B’C’ theo trường hợp góc – góc, từ đó suy ra các cặp tỉ số tương ứng của \(\widehat B\) và \(\widehat {B’}\) bằng nhau.

1. Ta đo được \(AB = 1,6cm,AC = 0,8cm,BC = 1,8cm\).
Tỉ số cạnh đối và cạnh huyền của góc B là:
\(\frac{{CA}}{{BC}} = \frac{{0,8}}{{1,8}} = \frac{4}{9}\).
Tỉ số cạnh kề và cạnh huyền của góc B là:
\(\frac{{BA}}{{BC}} = \frac{{1,6}}{{1,8}} = \frac{8}{9}\).
Tỉ số cạnh đối và cạnh kề của góc B là:
\(\frac{{CA}}{{AB}} = \frac{{0,8}}{{1,6}} = \frac{1}{2}\).
2. Ta đo được \(A’B’ = 2,4cm,A’C’ = 1,2cm,BC = 2,7cm\).
Tỉ số cạnh đối và cạnh huyền của góc B’ là:
\(\frac{{C’A’}}{{B’C’}} = \frac{{1,2}}{{2,7}} = \frac{4}{9}\).
Advertisements (Quảng cáo)
Tỉ số cạnh kề và cạnh huyền của góc B’ là:
\(\frac{{B’A’}}{{B’C’}} = \frac{{2,4}}{{2,7}} = \frac{8}{9}\).
Tỉ số cạnh đối và cạnh kề của góc B’ là:
\(\frac{{C’A’}}{{A’B’}} = \frac{{1,2}}{{2,4}} = \frac{1}{2}\).
Luyện tập1
Trả lời câu hỏi Luyện tập 1 trang 76
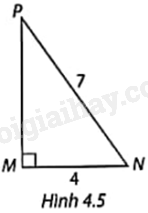
Tính các tỉ số lượng giác của góc N và góc P trong Hình 4.5.

Trong tam giác vuông có góc nhọn \(\alpha \), khi đó:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là \(\sin \alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là \(\cos \alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là \(\tan \alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là \(\cot \alpha \).

Tam giác MNP vuông tại M nên \(M{P^2} + M{N^2} = N{P^2}\) (Định lí Pythagore).
Suy ra: \(M{P^2} = N{P^2} - M{N^2} = {7^2} - {4^2} = 33\). Do đó, \(MP = \sqrt {33} \).
Do đó, \(\sin N = \frac{{MP}}{{PN}} = \frac{{\sqrt {33} }}{7}\), \(\cos N = \frac{{MN}}{{PN}} = \frac{4}{7}\), \(\tan N = \frac{{MP}}{{MN}} = \frac{{\sqrt {33} }}{4}\), \(\cot N = \frac{{MN}}{{MP}} = \frac{4}{{\sqrt {33} }}\).
\(\sin P = \frac{{MN}}{{PN}} = \frac{4}{7}\), \(\cos P = \frac{{MP}}{{PN}} = \frac{{\sqrt {33} }}{7}\), \(\tan P = \frac{{MN}}{{MP}} = \frac{4}{{\sqrt {33} }}\), \(\cot P = \frac{{MP}}{{MN}} = \frac{{\sqrt {33} }}{4}\).
