Hoạt động2
Trả lời câu hỏi Hoạt động 2 trang 76
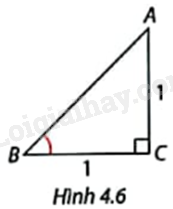
Trong Hình 4.6, tam giác ABC là tam giác gì? Xác định số đo và các tỉ số lượng giác của góc B.

Trong tam giác vuông có góc nhọn \(\alpha \), khi đó:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là \(\sin \alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là \(\cos \alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là \(\tan \alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là \(\cot \alpha \).

Tam giác ABC vuông tại C, \(CB = AC = 1\) nên tam giác ABC vuông cân tại C. Do đó, \(\widehat B = {45^o}\).
Tam giác ABC vuông tại C nên \(A{B^2} = B{C^2} + A{C^2} = {1^2} + {1^2} = 2\) (Định lí Pythagore).
Do đó, \(AB = \sqrt 2 \).
Suy ra, \(\sin B = \frac{{AC}}{{AB}} = \frac{1}{{\sqrt 2 }}\), \(\cos B = \frac{{BC}}{{AB}} = \frac{1}{{\sqrt 2 }}\), \(\tan B = \frac{{AC}}{{BC}} = 1\), \(\cot B = \frac{{BC}}{{AC}} = 1\).
Hoạt động3
Trả lời câu hỏi Hoạt động 3 trang 77
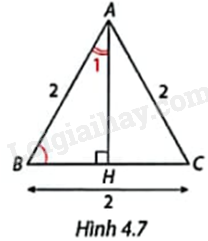
Trong Hình 4.7, tam giác ABC là tam giác gì? Xác định số đo và các tỉ số lượng giác của góc B và góc \({A_1}\).

Trong tam giác vuông có góc nhọn \(\alpha \), khi đó:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là \(\sin \alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là \(\cos \alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là \(\tan \alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là \(\cot \alpha \).
Advertisements (Quảng cáo)

Tam giác ABC có \(AB = BC = CA = 2\) nên tam giác ABC đều.
Do đó, AH là đường cao đồng thời là đường trung tuyến.
Do đó, \(BH = \frac{1}{2}BC = \frac{1}{2}.2 = 1\).
Tam giác AHB vuông tại H nên \(A{H^2} + H{B^2} = A{B^2}\) (Định lí Pythagore).
Suy ra: \(A{H^2} = A{B^2} - B{H^2} = {2^2} - {1^2} = 3\).
Do đó, \(AH = \sqrt 3 \)
Do đó, \(\sin B = \frac{{AH}}{{AB}} = \frac{{\sqrt 3 }}{2}\), \(\cos B = \frac{{BH}}{{AB}} = \frac{1}{2}\), \(\tan B = \frac{{AH}}{{BH}} = \frac{{\sqrt 3 }}{1} = \sqrt 3 \), \(\cot B = \frac{{BH}}{{AH}} = \frac{1}{{\sqrt 3 }}\).
\(\sin {A_1} = \frac{{BH}}{{AB}} = \frac{1}{2}\), \(\cos {A_1} = \frac{{AH}}{{AB}} = \frac{{\sqrt 3 }}{2}\), \(\tan {A_1} = \frac{{BH}}{{AH}} = \frac{1}{{\sqrt 3 }}\), \(\cot {A_1} = \frac{{AH}}{{BH}} = \frac{{\sqrt 3 }}{1} = \sqrt 3 \).
Tam giác ABC đều nên \(\widehat B = {60^o}\).
Tam giác AHB vuông tại H nên \(\widehat {{A_1}} = {90^o} - \widehat B = {30^o}\).
Luyện tập2
Trả lời câu hỏi Luyện tập 2 trang 77 SGK Toán 9
Trong Hình 4.9,hãy tính các tỉ số \(\frac{{PN}}{{PQ}}\) và \(\frac{{PN}}{{PM}}\), từ đó tìm \(\frac{{PQ}}{{PM}}\).
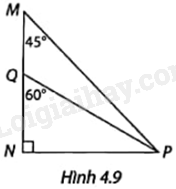

+ Xét tam giác NPQ vuông tại N có: \(\sin NQP = \frac{{PN}}{{PQ}}\), từ đó tính PQ theo PN và sin NQP.
+ Xét tam giác NPM vuông tại N có: \(\sin M = \frac{{NP}}{{MP}}\), từ đó tính MP theo PN và sinM.
+ Do đó, tính được tỉ số \(\frac{{PQ}}{{PM}}\)

Xét tam giác NPQ vuông tại N có:
\(\sin NQP = \frac{{PN}}{{PQ}}\) nên \(PQ = PN.\sin NQP = PN.\sin {60^o} = \frac{{\sqrt 3 }}{2}PN\).
Xét tam giác NPM vuông tại N có:
\(\sin M = \frac{{NP}}{{MP}}\), nên \(MP = PN.\sin M = PN.\sin {45^o} = \frac{{\sqrt 2 }}{2}PN\).
Do đó, \(\frac{{PQ}}{{PM}} = \frac{{\frac{{\sqrt 3 }}{2}PN}}{{\frac{{\sqrt 2 }}{2}PN}} = \frac{{\sqrt 6 }}{2}\)
