Hình nón có chiều cao \(h = a\), bán kính đáy \(R = \frac{{A’B’}}{2} = \frac{a}{2}\). + Thể tích hình nón chiều cao h. Phân tích và giải Giải bài tập 10.27 trang 109 SGK Toán 9 tập 2 - Kết nối tri thức - Bài tập cuối chương 10 . Cho hình lập phương ABCD.A’B’C’D’ cạnh a.
Câu hỏi/bài tập:

Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính thể tích của hình nón có đỉnh là tâm O của hình vuông ABCD và đáy là hình tròn tiếp xúc với các cạnh của hình vuông A’B’C’D’ (H.10.38).
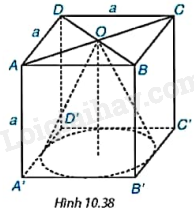

+ Hình nón có chiều cao \(h = a\), bán kính đáy \(R = \frac{{A’B’}}{2} = \frac{a}{2}\).
+ Thể tích hình nón chiều cao h, bán kính R là: \(V = \frac{1}{3}\pi {R^2}h\).
Advertisements (Quảng cáo)

Hình nón đã cho có chiều cao \(h = a\).
Vì đáy hình nón là đường tròn nội tiếp hình vuông A’B’C’D’ nên bán kính đáy là:
\(R = \frac{{A’B’}}{2} = \frac{a}{2}\).
Thể tích của hình nón là:
\(V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {\left( {\frac{a}{2}} \right)^2}a = \frac{{{a^3}\pi }}{{12}}\).
