Câu hỏi Thực hành 1 trang 114 Toán 9 Kết nối tri thức: Giải các phương trình sau: ${x^2} - 4x + 10 = 0$; $x + \frac{9}{{x - 1}} = 7$; c) \({x^2} - 2\left( {\sqrt 3...

Giải các phương trình sau:

a) ${x^2} - 4x + 10 = 0$;

b) $x + \frac{9}{{x - 1}} = 7$;

c) ${x^2} - 2\left( {\sqrt 3 - 1} \right)x - 2\sqrt 3 = 0$;

d) $\frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} = \frac{4}{{{x^2} - 1}}$.

+ Để giải phương trình nói chung, ta dùng lệnh Solve () hoặc Solutions () trên ô lệnh của cửa sổ CAS kết quả sẽ hiển thị ngay bên dưới.

+ Nghiệm của phương trình được biểu diễn dưới dạng tập hợp. Chú ý, kí hiệu {} thể hiện phương trình vô nghiệm.

a)

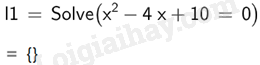
Vậy phương trình ${x^2} - 4x + 10 = 0$ vô nghiệm.

b)

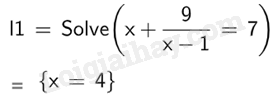
Vậy phương trình $x + \frac{9}{{x - 1}} = 7$ có nghiệm $x = 4$.

c)

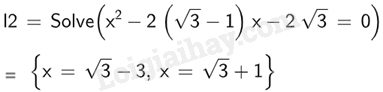
Vậy phương trình ${x^2} - 2\left( {\sqrt 3 - 1} \right)x - 2\sqrt 3 = 0$ có nghiệm $x = \sqrt 3 - 3;x = \sqrt 3 + 1$.

d)

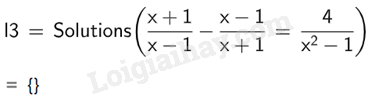
Vậy phương trình $\frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} = \frac{4}{{{x^2} - 1}}$ vô nghiệm.