Bài 37 trang 94 SGK Toán 9 tập 1,Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó....

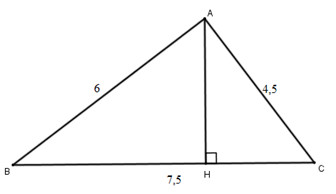
Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.

a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.

b) Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nắm trên đường nào?

Hướng dẫn làm bài:

a) Ta có: 6² + 4,5² = 36 + 20,25 = 56,25 = 7,5² = 56,25

∆ABC có AB² + AC² = BC² (=56,25) nên vuông tại A.

 \(\eqalign{& tgB = {{AC} \over {AB}} = {{4,5} \over 6} = 0,75 \Rightarrow \widehat B \approx {37^0} \cr & \widehat C = {90^0} - \widehat B \approx {53^0} \cr} \)

 ∆ABC vuông tại A, AH là đường cao nên:

AH.BC = AB.AC

 \( \Rightarrow AH = {{AB.AC} \over {BC}} = {{4,5.6} \over {7,5}} = 3,6(cm)\)

b) S_MBC = S_ABC ⇒ M cách BC một khoảng bằng AH.

Do đó M nằm trên hai đường thẳng song song cách BC một khoảng bằng 3,6 cm