Bài 6. Cho tam giác đều \(ABC\). Gọi \(O\) là tâm của đường tròn đi qua ba đỉnh \(A, B, C\).
a) Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính \(OA, OB, OC\).
b) Tính số đo các cung tạo bởi hai trong ba điểm \(A, B, C\).
Hướng dẫn giải:
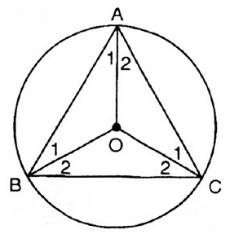
a) Ta có: \(\widehat A = \widehat B = \widehat C = {60^0}\) (gt)
Advertisements (Quảng cáo)
Suy ra: \(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{B_1}} = \widehat {{B_2}} = \widehat {{C_1}} = \widehat {{C_2}} = {30^0}\)
Tâm \(O\) của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều \(ABC\).
Suy ra: \(\widehat {AOB} = {180^0} - \widehat {{A_1}} - \widehat {{B_1}} = {180^0} - {30^0} - {30^0} = {120^0}\)
Tương tự ta suy ra: \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {120^0}\)
b) Từ \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {120^0}\) ta suy ra:
\(sđ\overparen{ABC}\) = \(sđ\overparen{BCA}\) = \(sđ\overparen{CAB}\) \(= 240^0\)
