
Biểu đồ sau ghi lại nhiệt độ lúc 12 giờ trưa tại một trạm quan trắc trong 10 ngày liên tiếp (đơn vị: 0C)
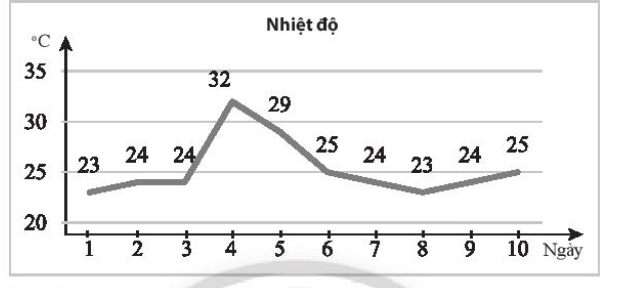
a) Hãy tìm viết mẫu số liệu thống kê nhiệt độ từ biểu đồ trên.
b) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu đó.
c) Hãy tìm phương sai và độ lệch chuẩn của mẫu số liệu đó.

Sắp xếp số liệu theo thứ tự không giảm và tìm khoảng biến thiên theo công thức\(R = {x_n} - {x_1}\)
Dùng kiến thức khoảng biến thiên và khoảng tứ phân vị, giá trị ngoại lệ đã học.
Tìm phương sai theo công thức \({S^2} = \frac{1}{n}\left( {{n_1}{x_1}^2 + {n_2}{x_2}^2 + ... + {n_k}{x_k}^2} \right) - {\overline x ^2}\) và độ lệch chuẩn \(S = \sqrt {{S^2}} \)

a) Mẫu số liệu:
|
Nhiệt độ |
23 |
Advertisements (Quảng cáo) 23 |
24 |
24 |
24 |
24 |
25 |
25 |
29 |
32 |
b)
+ Số cao nhất và thấp nhất lần lượt là 32 và 23 do đó khoảng biến thiên của dãy số liệu trên là: \(R = 32 - 23 = 9\)
+ Tứ phân vị: \({Q_2} = 24\); \({Q_1} = 24;{Q_3} = 25 \Rightarrow \Delta Q = {Q_3} - {Q_1} = 1\)
c)
+ Trung bình của mẫu số liệu là \(\overline x = 25,3\)
+ Phương sai: \({S^2} = 7,61\)
+ Độ lệch chuẩn: \(S = \sqrt {{S^2}} \approx 2,76\)
