
Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải các bất phương trình sau:
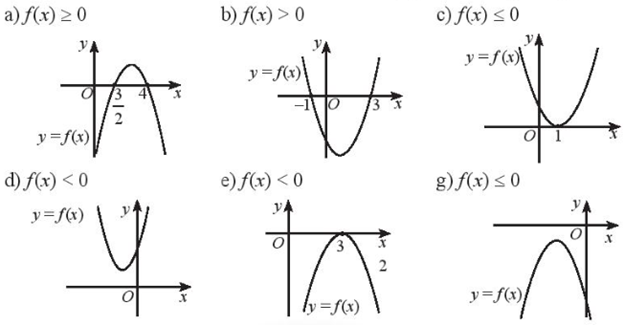

Dựa vào đồ thị ta xác định được nghiệm của bất phương trình
Phần đồ thị nằm trên trục hoành là phần hàm số có giá trị dương
Ngược lại phần đồ thị nằm dưới trục hoành là phần hàm số có giá trị âm

a) \(f\left( x \right) \ge 0\) khi và chỉ khi \(x \ge \frac{3}{2}\) và \(x \le 4\)
Advertisements (Quảng cáo)
Vậy tập nghiệm của bất phương trình là \(\left[ {\frac{3}{2};4} \right]\)
b) \(f\left( x \right) > 0\) khi và chỉ khi \(x < - 1\) hoặc \(x > 3\)
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\)
c) \(f\left( x \right) \le 0\) khi và chỉ khi \(x = 1\)
Vậy tập nghiệm của bất phương trình là \(\left\{ 1 \right\}\)
d) \(f\left( x \right) > 0\) với mọi \(x \in \mathbb{R}\). Tập nghiệm của bất phương trình \(f\left( x \right) < 0\) là \(\emptyset \)
e) \(f\left( x \right) < 0\) khi và chỉ khi \(x \ne 3\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\backslash \left\{ 3 \right\}\)
g) \(f\left( x \right) < 0\) với mọi \(x \in \mathbb{R}\). Tập nghiệm của bất phương trình \(f\left( x \right) \le 0\) là \(\mathbb{R}\)
