
Với mỗi hàm số dưới đây, hãy vẽ đồ thị, tập giá trị, khoảng đồng biến, khoảng nghịch biến của nó:
a) \(y = - {x^2} + 6x - 9\)
b) \(y = - {x^2} - 4x + 1\)
c) \(y = {x^2} + 4x\)
d) \(y = 2{x^2} + 2x + 1.\)

Cho hàm số \(y = a{x^2} +bx + c\)
- Xác định tọa độ đỉnh \(I(\frac {-b} {a};\frac {-\Delta} {4a})\)
- Trục đối xứng \(x=\frac {-b} {a}\)
- Giao với trục \(Ox,\,\,Oy.\)
- Xác định tập giá trị của hàm số
- Từ đồ thị tìm khoảng đồng biến, nghịch biến của hàm số

a) \(y = - {x^2} + 6x - 9\)
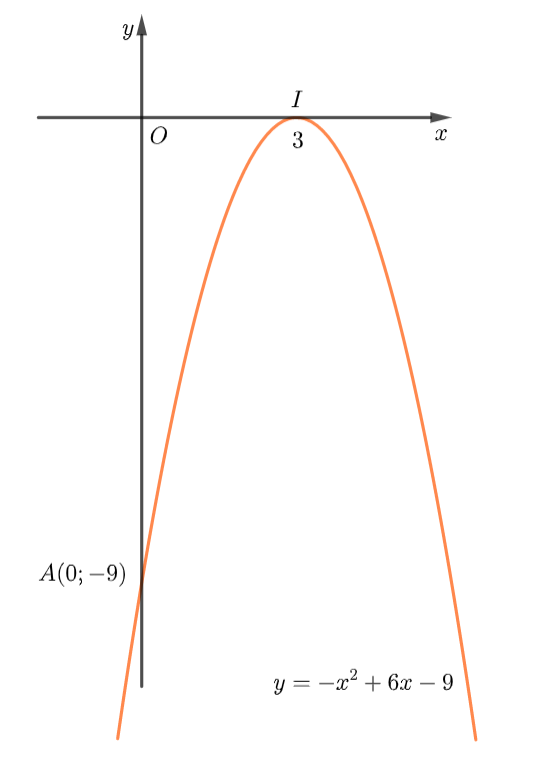
Ta có: \(a = - 1\) nên parabol quay bề lõm xuống dưới.
Đỉnh \(I\left( {3;0} \right).\) Trục đối xứng \(x = 3.\) Giao điểm của đồ thị với trục \(Oy\) là: \(A\left( {0; - 9} \right).\) Parabol cắt trục hoành tại \(x = 3.\)
Advertisements (Quảng cáo)
Tập giá trị của hàm số là: \(\left( { - \infty ;0} \right].\)
Từ đồ thị ta thấy: Hàm số \(y = - {x^2} + 6x - 9\) đồng biến trên khoảng \(\left( { - \infty ;3} \right)\) và nghịch biến trên khoảng \(\left( {3; + \infty } \right).\)
b) \(y = - {x^2} - 4x + 1\)
Ta có: \(a = - 1\) nên parabol quay bề lõm xuống dưới.
Đỉnh \(I\left( { - 2;5} \right).\) Trục đối xứng \(x = - 2.\) Giao điểm của hàm số với trục \(Oy\) là: \(\left( {0;1} \right).\) Giao điểm của hàm số với trục \(Ox\) là: \(x = - 2 + \sqrt 5 \) và \(x = - 2 - \sqrt 5 .\)
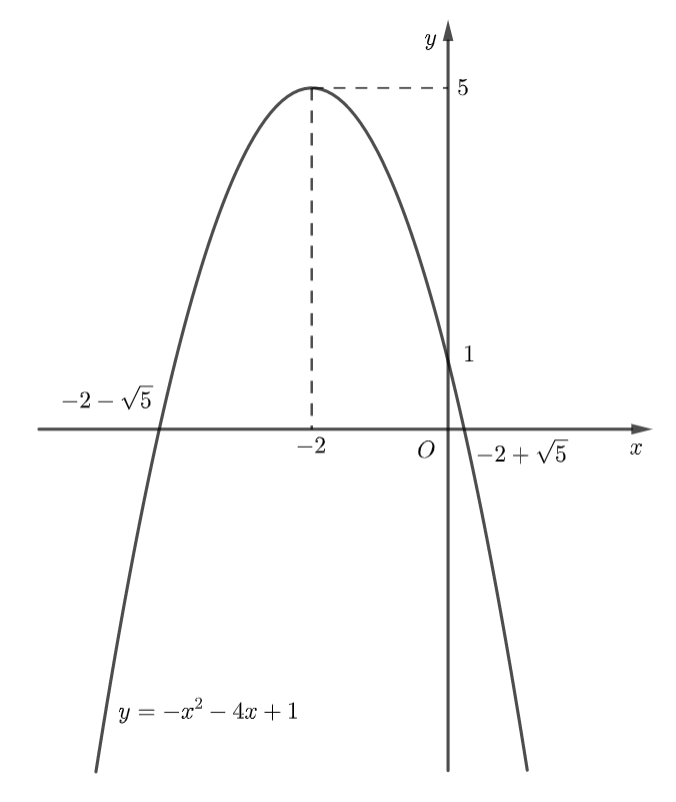
Tập giá trị của hàm số là: \(\left( { - \infty ;5} \right].\)
Từ đồ thị ta thấy: Hàm số \(y = - {x^2} - 4x + 1\) đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\) và nghịch biến trên khoảng \(\left( { - 2; + \infty } \right).\)
c) \(y = {x^2} + 4x\)
Ta có: \(a = 1 > 0\) nên parabol quay bề lõm lên trên.
Đỉnh \(I\left( { - 2; - 4} \right).\) Trục đối xứng \(x = - 2.\) Giao điểm của hàm số với trục \(Oy\) là: \(\left( {0;0} \right).\) Giao điểm của hàm số với trục \(Ox\) là: \(x = 0\) và \(x = - 4.\)
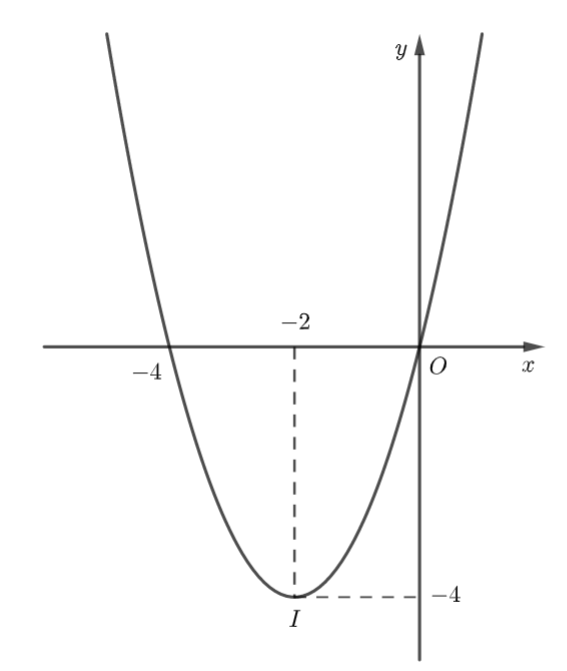
Tập giá trị của hàm số là: \(\left[ { - 4; + \infty } \right).\)
Từ đồ thị ta thấy: Hàm số \(y = {x^2} + 4x\) đồng biến trên khoảng \(\left( { - 2; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ; - 2} \right).\)
d) \(y = 2{x^2} + 2x + 1\)
Ta có: \(a = 2 > 0\) nên parabol quay bề lõm lên trên.
Đỉnh \(I\left( { - \frac{1}{2};\frac{1}{2}} \right).\) Trục đối xứng \(x = - \frac{1}{2}.\) giao điểm của hàm số với trục \(Oy\) là: \(\left( {0;1} \right).\) Đồ thị hàm số không có giao điểm với trục \(Ox.\) Lấy điểm \(\left( {1;5} \right)\) thuộc đồ thị hàm số, điểm đối xứng với điểm đó qua trục đối xứng \(x = - \frac{1}{2}\) là: \(\left( { - 2;5} \right).\)
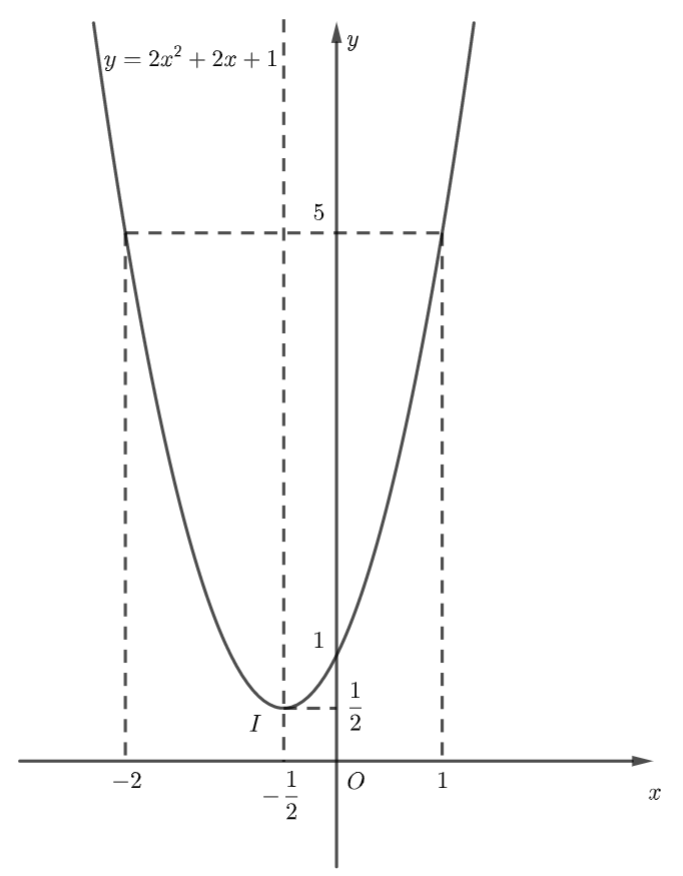
Tập giá trị của hàm số là: \(\left[ {\frac{1}{2}; + \infty } \right).\)
Từ đồ thị ta thấy: Hàm số \(y = 2{x^2} + 2x + 1\) đồng biến trên khoảng \(\left( { - \frac{1}{2}; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ; - \frac{1}{2}} \right).\)
