
Bảng sau thống kê số lượt chở khách mỗi ngày của một lái xe taxi trong 30 ngày.

a) Hãy tính số trung bình và mốt của mẫu số liệu trên.
b) Hãy lập bảng tần số ghép nhóm của mẫu số liệu trên với nhóm đầu tiên là \(\left[ {4,5;7,5} \right)\).
c) Hãy ước lượng số trung bình và mốt của mẫu số liệu ghép nhóm đó.

+ Sử dụng kiến thức về số trung bình của mẫu số liệu để tính:
Giả sử mẫu số liệu được cho dưới dạng bảng tần số ghép nhóm:
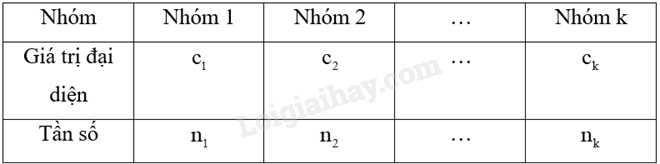
Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\overline x \), được tính như sau: \(\overline x = \frac{{{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}}}{n}\), trong đó \(n = {n_1} + {n_2} + ... + {n_k}\).
+ Sử dụng kiến thức về mốt của mẫu số liệu để tính: Giả sử nhóm chứa mốt là \(\left[ {{u_m};{u_{m + 1}}} \right)\), khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là \({M_O}\) được xác định bởi công thức: \({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right)\)

Advertisements (Quảng cáo)
a) Bảng tần số:

Số trung bình của mẫu số liệu là:
\(\left( {5{\rm{ + }}6.2 + 7 + 8.2 + 9.2 + 10.2 + 11.3 + 12.3 + 13.7 + 14 + 15.2 + 16{\rm{ + }}17 + 18.2} \right):30 = 11,7\)
Mốt của mẫu số liệu là 13.
b) Bảng tần số ghép nhóm là:

c) Bảng tần số ghép nhóm bao gồm các giá trị đại diện của nhóm là:
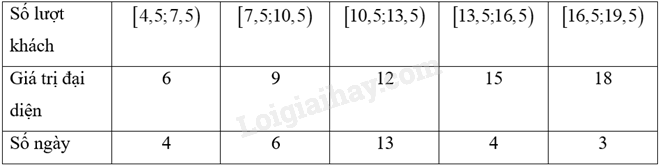
Số trung bình của mẫu số liệu ghép nhóm là: \(\overline x = \frac{{6.4 + 9.6 + 12.13 + 15.4 + 18.3}}{{4 + 6 + 13 + 4 + 3}} = 11,6\)
Nhóm chứa mốt của mẫu số liệu là \(\left[ {10,5;13,5} \right)\).
Do đó, \({u_m} = 10,5;{n_{m - 1}} = 6;{n_m} = 13,{n_{m + 1}} = 4,{u_{m + 1}} - {u_m} = 13,5 - 10,5 = 3\)
Mốt của mẫu số liệu ghép nhóm là: \({M_O} = 10,5 + \frac{{13 - 6}}{{\left( {13 - 6} \right) + \left( {13 - 4} \right)}}.3 = 11,8125\)
