Cho tam giác ABC. Tìm một điểm M trên cạnh AB và một điểm N trên cạnh AC sao cho MN song song với BC và AM = CN.

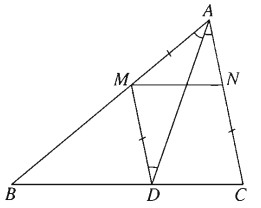
Giả sử đã dựng được hai điểm M, N thỏa mãn điều kiện đầu bài. Đường thẳng qua M và song song với AC cắt BC tại D. Khi đó tứ giác MNCD là hình bình hành. Do đó CN = DM. Từ đó suy ra tam giác AMD cân tại M. Do đó \(\widehat {MA{\rm{D}}} = \widehat {M{\rm{D}}A} = \widehat {DAC}\). Suy ra AD là phân giác trong của góc A. Do đó AD dựng được .Ta lại có \(\overrightarrow {NM} = \overrightarrow {C{\rm{D}}} \), nên có thể xem M là ảnh của N qua phép tịnh tiến theo vectơ \(\overrightarrow {DC} \).
Từ đó suy ra cách dựng:
Advertisements (Quảng cáo)
- Dựng đường phân giác trong của góc A. Đường này cắt BC tại D.
- Dựng đường thẳng d là ảnh của đường thẳng AC qua phép tịnh tiến theo vectơ \(\overrightarrow {C{\rm{D}}} \). d cắt AB tại M.
- Dựng N sao cho \(\overrightarrow {NM} = \overrightarrow {C{\rm{D}}} \).
Khi đó dễ thấy M, N thỏa mãn điều kiện đầu bài.
